表达式

奇异函数通常是指下列函数族：

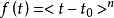
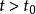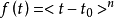当n>0或n=0时，且 时， ，否则 ;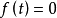

当n一般称为麦考利（W.H.Macauley）括号。

奇异函数在物理学中的应用在物理学中，经常要用处理一些包含某种无穷大的量以及不连续函数的微分等问题，因而引入一种“非正规函数”。这种函数最初于二十世纪三十年代，由著名物理学家狄拉克在量子力学研究中引入和定义。后来被命名为“狄里克δ函数”，简称为“δ函数”。五十年代法国数学家施瓦茨在深入研究δ函数性质的基础上，创立了分布论（亦即广义函数论）。他从理论上严格证实了不仅可以使用δ函数，而且还可以δ函数及其各阶导数，从而使δ函数理论趋于完整和严密。

常用奇异函数在物理学中，人们习惯的将包括δ函数的各阶导数，亥维赛（O.Heaviside）阶跃函数（简称为阶跃函数）及其各阶积分的函数族称为奇异函数。在物理学中，奇异函数应用最多的是阶跃函数u(t)和δ函数δ(t)。

应用举例用奇异函数表示某些理想化了的物理模型1

（1）力学中,集中量和分布量是经常遇到的两种物理模型。如集中质量和分布质量,瞬时作用力和持续力等等。集中量和分布量的差异,给使用基于连续函数的传统解法带来了限制,因而在传统的力学中,当遇到因集中量造成的不连续时,往往将对一个完整的问题的论述与表达进行分割和支离式的处理。实际上集中量与分布量可以用统一的方法来处理,所用的数学工具就是奇异函数。

（2）电路分析中,阶跃函数是常用函数。当要表示一分段表示的信号时,利用阶跃函数则一目了然。例如，可用阶跃函数表示理想化了的开关接通信号源的情况。当信号为脉冲形式,利用阶跃函数则使表达式变得简单。

2.利用奇异函数解决起始点跳变值的确定问题

3.在信号分析中，视奇异函数为单元函数，可把任一函数分解为奇异函数的和，此时用该分解求线性非时变系统的零状态响应。

奇异函数在材料力学中的应用在材料力学中,一般是用截面法及积分法来求解梁弯曲时的内力及变形。此法对于载荷在梁长度上连续变化时比较方便,但当梁上出现不连续载荷时,如一个梁上同时作用多个集中力、集中力偶及分布力时,则必须分段写出不同组的剪力和弯矩方程,常常导致很繁琐的结果。例如,在求解梁的变形时,当梁上外力情况复杂时,将梁分成n段,对于弯矩M(x)在不同区段内的表达式分别列出n个挠曲线微分方程;然后逐段分别积分两次,得到2n个积分常数,再由边界条件及连续条件求得。如果采用奇异函数,则可使某些问题的演算大为简化。由于奇异函数所表达出不连续性,那么,作为轴向位置函数的载荷集度(每单位长度的力)就能以一个方程的形式写出,直接积分就得到整个梁的剪力方程,而剪力方程的积分就得到整个梁的弯矩方程。这样,可根据一个方程直接观察到整个梁的内力情况。如果对弯矩方程再积分两次,则可得到一个方程表示整个梁的挠曲线,这时仅有两个积分常数需满足支坐边界条件2。

应用举例用奇异函数求解梁弯曲变形的问题。但在用奇异函数解该类题时应注意以下几点：

(1)奇异函数本身是不连续,而梁的各种状态的最终结果也仍然是不连续的；

(2)必须将坐标原点置于所研究梁的一端；

(3)须假想地将均布载荷k和线性分布载荷q(x)沿x轴正向延续至另一端,同时还要假想地加上与延续载荷的集度大小相等而方向相反的分布载荷,以保持原载荷作用不变；

(4)注意线性分布荷载q(x)的绝对值沿x轴的正负方向。

用奇异函数求解超静定梁的问题

在材料力学中,可以通过直接积分求解超静定梁。但当所受外力较为复杂时,此法演算较为繁琐,使用奇异函数可使得演算过程大大简化，且提高计算的准确性，另外一方面有利于计算机的编程。