在密码学中，ElGamal加密算法是一个基于迪菲-赫尔曼密钥交换的非对称加密算法。它在1985年由塔希尔·盖莫尔提出。[1]GnuPG和PGP等很多密码学系统中都应用到了ElGamal算法。

ElGamal加密算法可以定义在任何循环群G上。它的安全性取决于{G上的离散对数难题。

算法定义ElGamal算法，是一种较为常见的加密算法，它是基于1985年提出的公钥密码体制和椭圆曲线加密体系。既能用于数据加密也能用于数字签名，其安全性依赖于计算有限域上离散对数这一难题。在加密过程中，生成的密文长度是明文的两倍，且每次加密后都会在密文中生成一个随机数K，在密码中主要应用离散对数问题的几个性质：求解离散对数（可能）是困难的，而其逆运算指数运算可以应用平方-乘的方法有效地计算。也就是说，在适当的群G中，指数函数是单向函数。

算法ElGamal加密算法由三部分组成：密钥生成、加密和解密。

密钥生成密钥生成的步骤如下：

Alice利用生成元g产生一个q阶循环群G的有效描述。该循环群需要满足一定的安全性质。

Alice从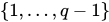 中随机选择一个 x。

Alice计算 。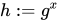

Alice公开h以及G,q,g的描述作为其公钥，并保留x作为其私钥。私钥必须保密。

加密使用Alice的公钥(G,q,g,h)向她加密一条消息m的加密算法工作方式如下：

Bob从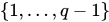 随机选择一个y，然后计算 。

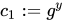Bob计算共享秘密 。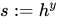

Bob把他要发送的秘密消息m映射为G上的一个元素m'。

Bob计算 。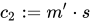

Bob将密文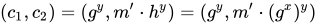 发送给Alice。

值得注意的是，如果一个人知道了m'，那么它很容易就能知道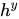 的值。因此对每一条信息都产生一个新的y可以提高安全性。所以y也被称作临时密钥。

解密利用私钥x对密文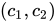 进行解密的算法工作方式如下：

Alice计算共享秘密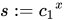

然后计算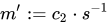 ，并将其映射回明文 m，其中 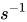是s在群G上的逆元。（例如：如果G是整数模n乘法群的一个子群，那么逆元就是模逆元）。

解密算法是能够正确解密出明文的，因为

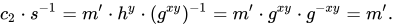
实际使用ElGamal加密系统通常应用在混合加密系统中。例如：用对称加密体制来加密消息，然后利用ElGamal加密算法传递密钥。这是因为在同等安全等级下，ElGamal加密算法作为一种非对称密码学系统，通常比对称加密体制要慢。对称加密算法的密钥和要传递的消息相比通常要短得多，所以相比之下使用ElGamal加密密钥然后用对称加密来加密任意长度的消息，这样要更快一些1。

数字签名方案在系统中有两个用户A和B，A要发送消息到B，并对发送的消息进行签名。B收到A发送的消息和签名后进行验证。

系统初始化选取一个大的素数p，g是GF(p)的本原元。h：GF(p)→GF(p)，是一个单向Hash函数。系统将参数p、g和h存放于公用的文件中，在系统中的每一个用户都可以从公开的文件中获得上述参数。

数字签名假定用户A要向B发送消息m [1,p-1]，并对消息m签字。第一步：用户A选取一个x [1,p-1]作为秘密密钥，计算y= (mod p)作为公钥。将公钥y存放于公用的文件中。第二步：随机选取k [1,p-1]且gcd(k,(p-1))=1，计算r= (mod p)。对一般的ElGamal型数字签名方案有签名方程（Signature Equation）：ax=bk+c(mod(p-1))。

其中(a，b，c)是(h(m),r,s)数学组合的一个置换。由签名方程可以解出s。那么(m,(r,s))就是A对消息m的数字签名。第三步：A将(m,(r,s))发送到B

签名验证当B接收到A发送的消息(m,(r,s))，再从系统公开文件和A的公开文件中获得系统公用参数p，g，h和A的公钥y。由(m,(r,s))计算出(a，b，c)验证等式：y^r·r^s = g^m(mod p)是否成立。

D.Bleichenbache“GeneratingElGamal Signatures Without Knowing the Secret Key”中提到了一些攻击方法和对策。ElGamal的一个不足之处是它的密文成倍扩张。

美国的DSS(Digital Signature Standard)的DSA(Digital Signature Algorithm)算法是经ElGamal算法演

变而来。

本词条内容贡献者为:

闫晓东 - 副教授 - 中央民族大学信息工程学院