等差数列是常见数列的一种,可以用AP表示,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列,而这个常数叫做等差数列的公差,公差常用字母d表示1。例如:1,3,5,7,9……(2n-1)。等差数列{an}的通项公式为:an=a1+(n-1)d。前n项和公式为:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/22。注意: 以上整数。
一般定义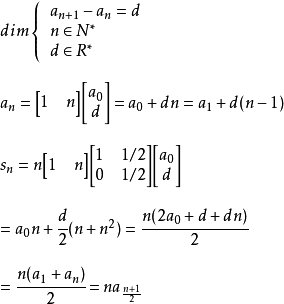
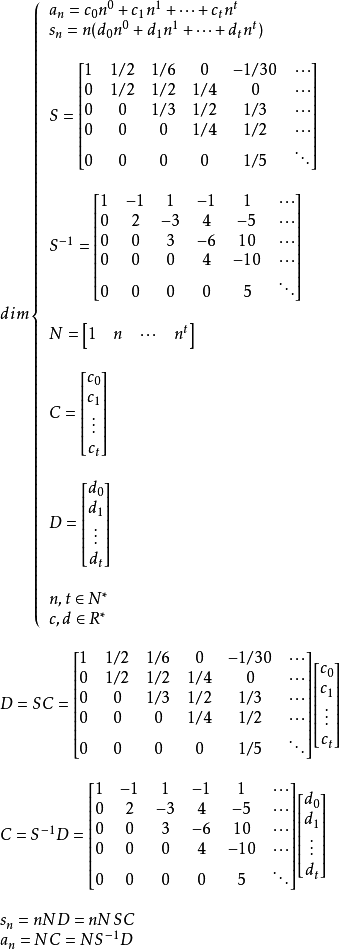
等差数列是多项式数列的特殊形式
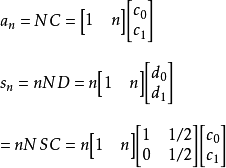
例题1
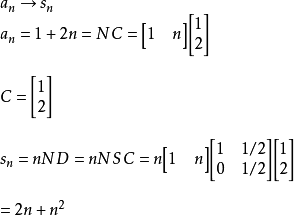
例题2
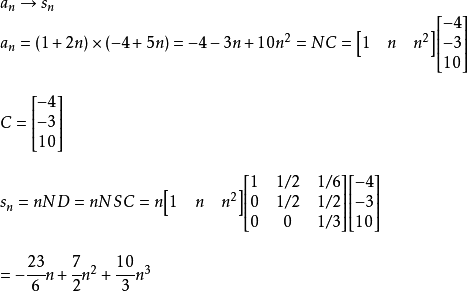
例题3
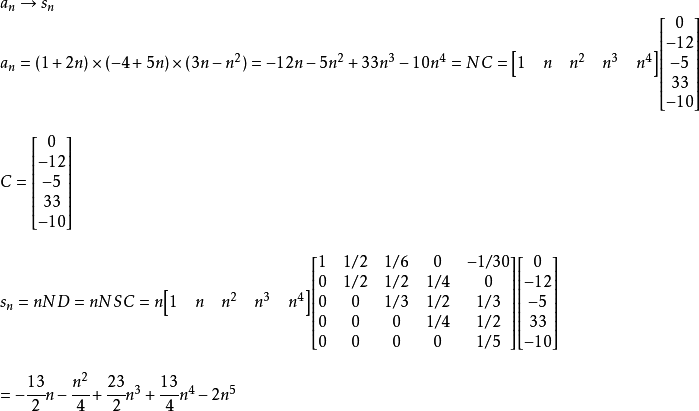
证明

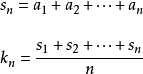
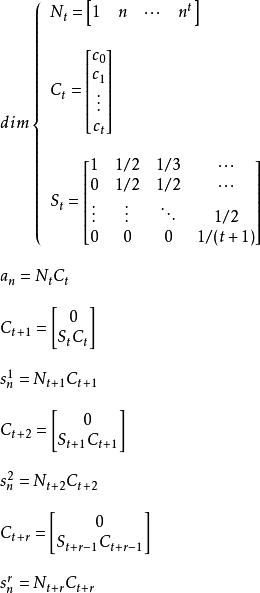
凯森和可以如下表示
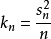
首项: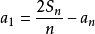 /末项-(项数-1)×公差
/末项-(项数-1)×公差
末项: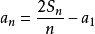
通项公式: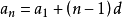
项数: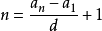
公差: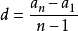
如:数列1,3,5,7,……,97,99 公差就是d=3-1=2 将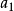 推广到
推广到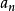 ,则为:
,则为: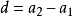
a1,a2,a3....an,n=奇数,Sn=(a((n-1)/2))*((n-1)/2)3
特殊性质1.在数列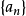 中,若
中,若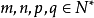 ,则有:
,则有:
①若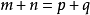 ,则am+an=ap+aq.
,则am+an=ap+aq.
②若m+n=2q,则am+an=2aq.
2.在等差数列中,若Sn为该数列的前n项和,S2n为该数列的前2n项和,S3n为该数列的前3n项和,则Sn,S2n-Sn,S3n-S2n也为等差数列4。
求和公式设首项为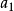 , 末项为
, 末项为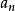 , 项数为
, 项数为 , 公差为
, 公差为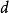 , 前
, 前 项和为
项和为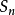 , 则有5:
, 则有5:
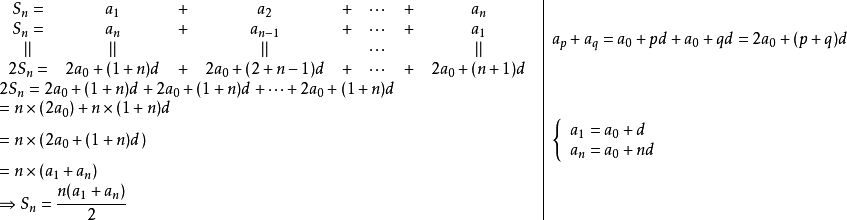
①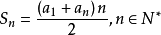 ;
;
②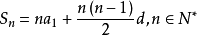 ;
;
③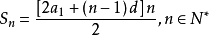 ;
;
④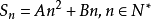 , 其中
, 其中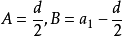 ..
..
当d≠0时,Sn是n的二次函数,(n,Sn)是二次函数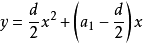 的图象上一群孤立的点。利用其几何意义可求前n项和Sn的最值。
的图象上一群孤立的点。利用其几何意义可求前n项和Sn的最值。
注意:公式一二三事实上是等价的,在公式一中不必要求公差等于一。
本词条内容贡献者为:
杨磊 - 副教授 - 北京大学数学学院


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

