平方平均数（quadratic mean），又名均方根（Root Mean Square），是指一组数据的平方的平均数的算术平方根。

定义一组数据的平方的平均数的算术平方根叫做平方平均数。公式如下：

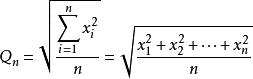
平方平均数（quadratic mean）又名均方根（Root Mean Square），英文缩写为RMS。它是2次方的广义平均数的表达式，也可称为2次幂平均数。英文名为，一般缩写成RMS。

公式下面是平方平均数不小于于算术平均数的证明：

由柯西不等式，得

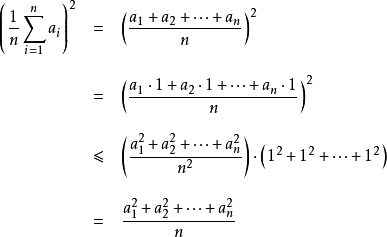
所以

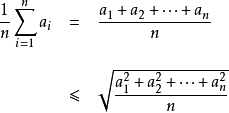
适用模型方均根值并非所有模型均适用， 只有在数值分布呈现正态分布时才适用。

如果分布呈现方波、三角波，那就要用其他的公式， 否则失真会很大。

国（初）中、高中的数学题目中常常会出现以方均根值计算班级平均成绩的题目， 这是预先假设全班成绩为正态分布的结果，实际情况不一定完全适用。 如成绩分布极为平均或呈现多峰状（如30分、70分的人数远超过其他分数的人数）， 方均根值就无法真实表现出该班级的平均成绩。1

参见算术平均数

几何平均数

调和平均数

算术-几何平均数

平均数不等式

最小二乘法

均方差

数学符号表

本词条内容贡献者为:

胡启洲 - 副教授 - 南京理工大学