无穷小就是以数零为极限的变量。然而常量是变量的特殊一类,就像直线属于曲线的一种。因此常量也是可以当做变量来研究的。这么说来——0是可以作为无穷小的常数。从另一方面来说,等价无穷小也可以看成是泰勒公式在零点展开到一阶的泰勒展开公式。
定义极限为零的变量称为无穷小量,简称无穷小。等价无穷小替换是计算未定型极限的常用方法,它可以使求极限问题化繁为简,化难为易。
求极限时使用等价无穷小的条件:一个是被代换的量,在去极限的时候极限值为0;另一个是被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。1
等价无穷小的定义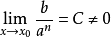 (C为常数),就说b是a的n阶的无穷小, b和a^n是同阶无穷小。特殊地,C=1且n=1,即
(C为常数),就说b是a的n阶的无穷小, b和a^n是同阶无穷小。特殊地,C=1且n=1,即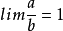 ,则称a和b是等价无穷小的关系,记作a~b。2
,则称a和b是等价无穷小的关系,记作a~b。2
假设a、b都是在x的同一变化过程(x→x0、x→∞、x→x0+……)时的无穷小,且
(1)如果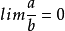 ,就说a是比b高阶的无穷小(或b是a低阶的无穷小),记作a=o(b)
,就说a是比b高阶的无穷小(或b是a低阶的无穷小),记作a=o(b)
(2)如果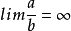 ,就是说a是比b低阶的无穷小。
,就是说a是比b低阶的无穷小。
比如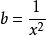 ,
,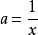 。x→∞时,通俗的说,b任意时刻都比a更快地趋于0,所以称做是b高阶。假如有
。x→∞时,通俗的说,b任意时刻都比a更快地趋于0,所以称做是b高阶。假如有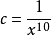 ,那么c比a和b都要高阶,因为c更快地趋于0了。
,那么c比a和b都要高阶,因为c更快地趋于0了。
如果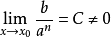 (C为常数),就说b是关于a的n阶的无穷小, b和a^n是同阶无穷小。3
(C为常数),就说b是关于a的n阶的无穷小, b和a^n是同阶无穷小。3
确切地说,当函数中自变量x或数列中n无限接近某个值x0(x0可以是0、∞、或是别的什么数)时,函数值f(x)与零无限接近,即limf(x)=0,则称f(x)为当x→x0时的无穷小或无穷小量。
例如,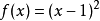 是当x→1时的无穷小量,f(n)=1/n是当n→∞时的无穷小量,f(x)=sinx是当x→0时的无穷小量。特别要指出的是,切不可把很小的常数与无穷小量混为一谈,常数0在自变量所有过程中都是无穷小,但是无穷小不一定是0。
是当x→1时的无穷小量,f(n)=1/n是当n→∞时的无穷小量,f(x)=sinx是当x→0时的无穷小量。特别要指出的是,切不可把很小的常数与无穷小量混为一谈,常数0在自变量所有过程中都是无穷小,但是无穷小不一定是0。
设在x的某一变化过程中,α和β都是无穷小,且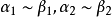 ,
,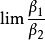 存在(不包括
存在(不包括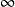 ),
),
则: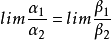
注意:
①等价无穷小一般只能在乘除中替换,在加减中替换有时会出错(加减时可以整体代换,不一定能随意单独代换或分别代换),比如mf(x)+ng(x),只有f(x)/g(x)的极限不是-n/m时,才可进行等价无穷小代换。1
②上各式中的x可以是f(x)也可以新变量t,如 f(x)→0,sin(f(x))~f(x)仍成立。
可直接等价替换的类型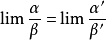
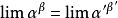
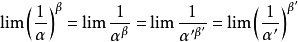
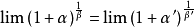
(以上几个性质可以用来化简一些未定式以方便运用洛必达法则)
需要满足一定条件才能替换的类型若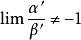 ,则
,则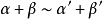
(该条性质非常重要,这是判断在加减法中能否分别等价替换的重要依据)
变上限积分函数(积分变限函数)也可以用等价无穷小进行替换。
等价无穷小公式当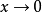 时,
时,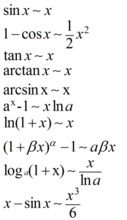
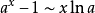
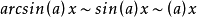
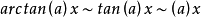
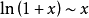
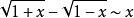
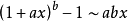
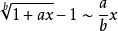
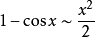
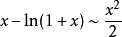
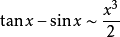
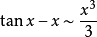
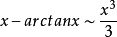
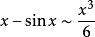
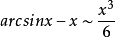
注:以上各式可通过泰勒展开式推导出来。
推导过程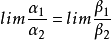 α和β都是无穷小,且
α和β都是无穷小,且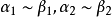 ,
,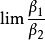 存在(或
存在(或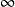 ),则有
),则有
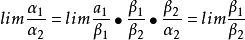 4
4
数学分析的基础概念。它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的数值(极限值)。极限方法是数学分析用以研究函数的基本方法,分析的各种基本概念(连续、微分、积分和级数)都是建立在极限概念的基础之上,然后才有分析的全部理论、计算和应用.所以极限概念的精确定义是十分必要的,它是涉及分析的理论和计算是否可靠的根本问题。历史上是柯西(Cauchy,A.-L.)首先较为明确地给出了极限的一般定义。他说,“当为同一个变量所有的一系列值无限趋近于某个定值,并且最终与它的差要多小就有多小”(《分析教程》,1821),这个定值就称为这个变量的极限.其后,外尔斯特拉斯(Weierstrass,K.(T.W.))按照这个思想给出严格定量的极限定义,这就是现在数学分析中使用的ε-δ定义或ε-Ν定义等。从此,各种极限问题才有了切实可行的判别准则。在分析学的其他学科中,极限的概念也有同样的重要性,在泛函分析和点集拓扑等学科中还有一些推广。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

