求解方程组时如果对数据进行较小的扰动，则得出的结果具有很大波动，这样的矩阵称为病态矩阵。

在求解任何反问题的过程中通常会遇到病态矩阵问题，而且病态矩阵问题还未有很好的解决方法，尤其是长方形、大型矩阵。目前主要有Tikhonov、奇异值截断、奇异值修正、迭代法等方法。

简介病态矩阵是一种特殊矩阵。指条件数很大的非奇异矩阵。病态矩阵的逆和以其为系数矩阵的方程组的界对微小扰动十分敏感，对数值求解会带来很大困难。1

在求解任何反问题的过程中通常会遇到病态矩阵问题，而且病态矩阵问题还未有很好的解决方法，尤其是长方形、大型矩阵。目前主要有Tikhonov、奇异值截断、奇异值修正、迭代法等方法。

求解方法求解方程组时对数据的小扰动很敏感的矩阵。

解线性方程组Ax=b时，若对于系数矩阵A及右端项b的小扰动 δA、δb，方程组 (A+δA)χ=b+δb的解 χ 与原方程组Ax=b的解差别很大，则称矩阵A为病态矩阵。方程组的近似解 χ 一般都不可能恰好使剩余 r=b-Aχ 为零，这时 χ 亦可看作小扰动问题Aχ=b-r(即δA=0，δb=-r) 的解，所以当A为病态时，即使剩余很小，仍可能得到一个与真解相差很大的近似解。

判定方法判定矩阵是否病态以及衡量矩阵的病态程度通常是看矩阵A的条件数K(A)=‖A-1‖*‖A‖ 的大小，其中 A-1 为矩阵 A 的逆， ‖‖ 表示对矩阵取某一种范数。 K(A) 称为 A 的条件数，它很大时，称 A 为病态，否则称良态； K(A) 愈大， A 的病态程度就愈严重。

对小扰动问题 (A+δA)χ=b+δb 与原问题 Ax=b 的解有估计式

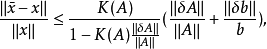
对矩阵求逆亦有估计式从上估计式可以看出条件数对解方程组及矩阵求逆的影响。

希尔伯特矩阵是一类著名的病态矩阵，其定义为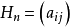。式中。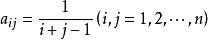

由于Hn对称正定，当取 ‖Hn‖ 为欧氏范数时，K(Hn) 即为Hn 的最大与最小特征值之比。对n=7,8,9,10有K(H7)=4.75×108，K(H8)=1.53×1010，K(H9)=4.93×1011，K(H10)=1.60×1013。

当n较大时，有近似表达式K(Hn)～e3.5n。在一台相当于 10 位十进制字长的计算机上对希尔伯特矩阵求逆或解方程组时，如 n≥8 ，则所得解答连一位准确数字都没有。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学