分部积分法是微积分学中的一类重要的、基本的计算积分的方法。它的主要原理是利用两个相乘函数的微分公式,将所要求的积分转化为另外较为简单的函数的积分。根据组成被积函数的基本函数类型,将分部积分的顺序整理为口诀:“反对幂三指”。分别代指五类基本函数:反三角函数、对数函数、幂函数、三角函数、指数函数的积分。1
公式推导设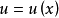 及
及 是两个关于
是两个关于 的函数,各自具有连续导数
的函数,各自具有连续导数 及
及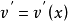 ,则按照乘积函数求微分法则,则有1
,则按照乘积函数求微分法则,则有1
 或者
或者
 对其两边进行积分,且因
对其两边进行积分,且因 的原函数是
的原函数是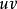 ,得
,得
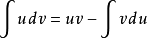
如果将 和
和 用微分形式写出,则亦可得出
用微分形式写出,则亦可得出
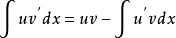 上两式就表示出了分部积分法则。它把
上两式就表示出了分部积分法则。它把 的积分化为
的积分化为 的积分,也即分部积分的好处是,可将复杂的被积函数简化为另一较易求得的函数积分。
的积分,也即分部积分的好处是,可将复杂的被积函数简化为另一较易求得的函数积分。
例如,要求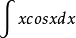 ,则依分部积分法则,令
,则依分部积分法则,令
 如此
如此
 则按上述公式有
则按上述公式有

四种典型模式一般地,从要求的积分式中将 凑成
凑成 是容易的,但通常有原则可依,也就是说不当的分部变换不仅不会使被积分式得到精简,而且可能会更麻烦。分部积分法最重要之处就在于准确地选取
是容易的,但通常有原则可依,也就是说不当的分部变换不仅不会使被积分式得到精简,而且可能会更麻烦。分部积分法最重要之处就在于准确地选取 ,因为一旦
,因为一旦 确定,则公式中右边第二项
确定,则公式中右边第二项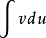 中的
中的 也随之确定,但为了使式子得到精简,如何选取
也随之确定,但为了使式子得到精简,如何选取 则要依
则要依 的复杂程度决定,也就是说,选取的
的复杂程度决定,也就是说,选取的 一定要使
一定要使 比之前的形式更简单或更有利于求得积分。依照经验,可以得到下面四种典型的模式。2记忆模式口诀:反(函数)对(数函数)幂(函数)三(角函数)指(数函数)。
比之前的形式更简单或更有利于求得积分。依照经验,可以得到下面四种典型的模式。2记忆模式口诀:反(函数)对(数函数)幂(函数)三(角函数)指(数函数)。
模式一通过对 求微分后,
求微分后, 中的
中的 比
比 更加简洁,而
更加简洁,而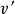 与
与 的类型相似或复杂程度相当。
的类型相似或复杂程度相当。
例如,对于形如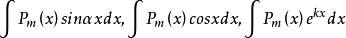 的不定积分(其中
的不定积分(其中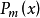 为
为 次多项式),由于对多项式求微分可以降次,且三角函数或指函数的积分则较容易求得,所以可以令
次多项式),由于对多项式求微分可以降次,且三角函数或指函数的积分则较容易求得,所以可以令 ,而将另一个函数看成
,而将另一个函数看成 通过分部求得积分。2
通过分部求得积分。2
例如 求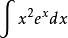
首先,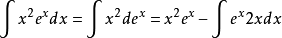
对该式第二项再按此模式进行分部积分,得

故原式
模式二通过对 求微分使得它的类型与
求微分使得它的类型与 的类型相同或相近,然后将它们作为一个统一的函数来处理。例如对形如
的类型相同或相近,然后将它们作为一个统一的函数来处理。例如对形如 等的积分,总是令
等的积分,总是令 ,则
,则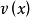 则为一个
则为一个 次的多项式,另一个函数(
次的多项式,另一个函数( 等)看成
等)看成 。通过分部积分,很容易求出不定积分。2
。通过分部积分,很容易求出不定积分。2
例如,求
 而该式第二项为
而该式第二项为

故原积分式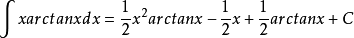
模式三利用有些函数经一次或二次求微分后不变的性质,通过一次或二次分部积分后,使等式右端再次产生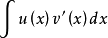 ,只要它的系数不为1,就可以利用解方程的方法求出原积分
,只要它的系数不为1,就可以利用解方程的方法求出原积分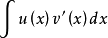 。2
。2
例如,对于积分 和
和
按法则对他们进行分部积分得


这样,所求积分均由另一个积分所表示出来,将这两式相加和相减(即解方程)得到所求积分表达式
 以及
以及
 这两个通用表达式就可以求出该类型的所有积分式,比如
这两个通用表达式就可以求出该类型的所有积分式,比如

模式四对某些形如 的不定积分,利用分部积分可降低
的不定积分,利用分部积分可降低 的次数,求得递推公式,然后再次利用递推公式,求出
的次数,求得递推公式,然后再次利用递推公式,求出 。1
。1
例如,对于积分
当 时,
时,
当 时,
时,
而该式的第二项又可变换为3
 将其带入上式,则得到
将其带入上式,则得到
 故
故
 最后,得到统一的递推关系式
最后,得到统一的递推关系式
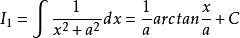
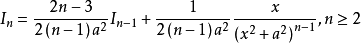
定积分与不定积分的分部积分法一样,可得1

简写为
例如
示例例1:
例24:



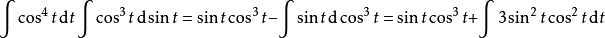



回代即可得到 的值。
的值。
本词条内容贡献者为:
胡建平 - 副教授 - 西北工业大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

