柯西-施瓦茨不等式是一个在众多背景下都有应用的不等式，例如线性代数，数学分析，概率论，向量代数以及其他许多领域。它被认为是数学中最重要的不等式之一。此不等式最初于1821年被柯西提出，其积分形式在1859被布尼亚克夫斯基提出，而积分形式的现代证明则由施瓦兹于1888年给出。

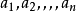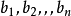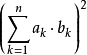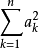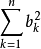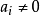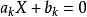简介定理（柯西-施瓦茨不等式）：若 和 是任意实数，则有 ≤（ ）（ ）此外，如果有某个，则上式中的等号当且仅当存在一个实数X使得对于每一个都有时成立。1

证明证明1平方和绝不可能是负数，故对每一个实数X都有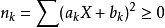其中，等号当且仅当每一项都等于0时成立。

数学上，柯西—施瓦茨不等式，又称施瓦茨不等式或柯西—布尼亚科夫斯基—施瓦茨不等式，是一条很多场合都用得上的不等式，例如线性代数的矢量，数学分析的无穷级数和乘积的积分，和概率论的方差和协方差。不等式以奥古斯丁·路易·柯西（Augustin Louis Cauchy），赫尔曼·阿曼杜斯·施瓦茨（Hermann Amandus Schwarz），和维克托·雅科夫列维奇·布尼亚科夫斯基（Виктор Яковлевич Буняковский）命名。

证明2柯西—施瓦茨不等式说，若x和y是实或复内积空间的元素，那么

等式成立当且仅当x和y是线性相关。

柯西—施瓦茨不等式的一个重要结果，是内积为连续函数。2

证明3柯西—施瓦茨不等式有另一形式，可以用范的写法表示：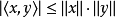

应用实内积空间的情形注意到y = 0时不等式显然成立，所以可假设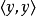 非零。对任意 ，可知

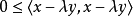
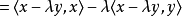
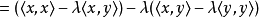
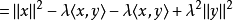
现在取值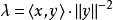 ，代入後得到

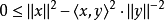
因此有

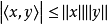
复内积空间的情形证明类上。对任意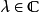 ，可知

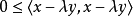
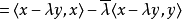
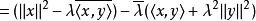
现在取值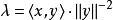 ，代入後得到

因此有

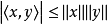
特例对欧几里得空间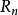，有

对平方可积的复值函数，有

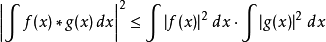
这两例可更一般化为赫尔德不等式。

在3维空间，有一个较强结果值得注意：原不等式可以增强至等式

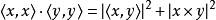
本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学