机架横梁机是一种冶金的专业术语，是指型材成型机上横梁和机架连接装置，涉及型材成型机的设计和制造技术。

概念机架横梁是指在机架上固定连接轴，左、右机架上装一根上横梁，上横梁套在连接轴上，在连接轴的卡槽中插有插板。通过无螺栓连接，拆卸插板，就能很方便地拆卸上横梁，拆下上辊轴、下辊轴，完成换辊工作，可节省大量的换辊时间，降低劳动强度，提高工作效率。

闭式机架横梁静不定力矩的柔性转角计算法用材料力学方法计算闭式机架横梁的静不定力矩时，由于对机架建立的矩形自由框架模型假设机架横梁与立柱转角处是刚性的，忽略了机架转角处的变形，计算结果偏离实际情况。研究提出一种柔性转角计算法。考虑机架横梁与立柱转角处存在的角变形，并利用该角变形与所受弯矩的关系，求出横梁静不定力矩和角变形的关系，进而通过卡氏定理求解，得出横梁静不定力矩的函数表达式。本方法经过实例检验，计算数值结果有足够高的精度，并且避免了冗长的数值运算，可以作为建立更复杂控制模型的基础工具。

柔性转角计算法计算上横梁中部的静不定力矩时，因方法的差别而导致不同的结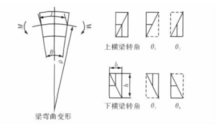果，但是当静不定力矩数值求解出来后，其他诸如各个特征点的应力、应变和位移的计算过程，各种计算方法则大致相同。本方法认为机架转角处存在附加的、相对的转角变形，并且是可以计算出来的。转角变形量的大小和立柱上的力矩直接相关，呈线性正比例关系。转角变形量由四个部分组成，分别是力矩对上横梁、立柱上部、立柱下部、下横梁产生的变形。对应的变形值分别用θ1、θ2、θ3和θ4表示，如图1所示。

将机架横梁看作纯弯曲梁，受弯后的转角和受弯时的中性层曲率半径分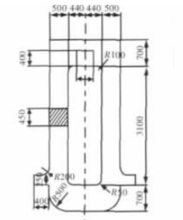别用下式计算。

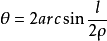
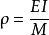式中，l为弯曲梁长度；θ为弯曲梁受弯后的转角，即角变形量；ρ为弯曲梁中性层曲率半径；E为材料弹性横量；I为惯性力矩；M为弯曲梁的弯矩。

上、下横梁和立柱上、下部都可以看作特殊形式的纯弯曲梁，呈倒三角形布置，其弯曲变形是由纵向平行侧面构成的长方体纯弯曲梁的二分之一，因而转角变形量也相应减半。

计算实例图2为某轧钢厂750 mm四辊冷轧机机架。研究分别用材料力学法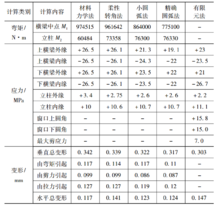、小圆弧法、精确圆弧法、有限元法以和柔性转角法对该机架进行强度计算。计算结果见表1。

表1中用材料力学法和柔性转角法计算的M1与M2的总和相同。柔性转角法计算出的M1比材料力学法小，因而M2能大些。但是M2更接近小圆弧法和精确圆弧法的计算结果。小圆弧法和精确圆弧法计算的M1与M2要小，导致计算出的横梁外缘应力数据偏小。

由于材料力学法和柔性转角法忽略了上下横梁的形状差异，应力计算结果表明上下横梁内外缘应力数据为对称分布，与实际情况有较大差别。小圆弧法和精确圆弧法可以如实地反映机架真实的形状及变化过程，上横梁内外缘应力数据应该和上横梁内外缘应力数据有所不同，所以计算结果大部分与有限元法比较接近。

精确圆弧法计算的垂直方向变形最接近有限元法计算结果，而水平方向变形的计算则以柔性转角法最为准确。

研究结论柔性转角法与材料力学法、小圆弧法和精确圆弧法都是闭式轧机机架的解析算法。材料力学法算法简单，计算结果偏于保守; 小圆弧法和精确圆弧法计算过程冗长、模型分段复杂，计算结果相对准确; 柔性转角法算法比较简单，计算结果也比较准确，有一定的参考价值。1

斜辊矫直机铸焊式机架横梁的优化分析斜辊矫直机用于矫直钢管与圆棒料，使轧件在螺旋前进过程中各断面受到多次弹塑性弯曲，最终改善轧件的弯曲度和断面的椭圆度。机架是斜辊矫直机的重要部件，也是矫直机中一个关键的、非更换的永久性部件，其结构、受力状况和使用工况都比较复杂，承受着矫直机工作时的全部载荷。

斜辊矫直机通常采用组合式预应力机架，由上、下横梁和立柱系统组成，其中上、下横梁是矫直机机架的关键组成部分，其强度与刚度直接影响着矫直机的寿命与矫直产品的质量。横梁的设计除要确保矫直机机架在使用过程中的安全性和合理的寿命外，还要考虑制造工艺的简化。鉴于此，如何合理可靠地计算横梁强度和刚度是矫直机机架设计时必须解决的重要问题。

以往的矫直机上、下横梁大多设计为铸件，铸件的制造周期长，单件生产成本高，又容易产生铸造缺陷。多采用铸焊结构，而因横梁内部有很多筋板，计算较为复杂。设计时机架力学分析的主要方法是应用简支梁简化模型， 将横梁的受力及截面进行简化，虽然能够得出横梁大约尺寸（如横梁厚度、上下板厚度等），但不能获得其内部受力与变形分布的细节；因此，要想从设计环节提高产品质量，对上、下横梁进行模拟仿真分析是十分必要的。2

矫直机机架以一条不锈钢钢管六辊矫直机生产线的工程项目为例，通过有限元结构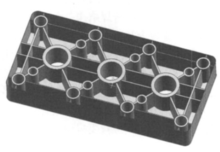分析软件ANSYS对矫直机机架模型进行模拟仿真分析及优化。该项目矫直机机架如图3所示，其为立式结构，上横梁装有压下机构及上矫直辊组，下横梁装有反弯机构及下矫直辊组。根据结构需要，下横梁需设置地脚孔，使整个机架固定在地基上，故设计时其厚度比上横梁厚很多。在上、下横梁受力相同的前提下可以得出，该矫直机机架上横梁的刚度、强度比下横梁低；因此，本文只对上横梁进行优化分析。

机架上横梁三维模型及分析（1）三维建模

根据要矫直的管棒材规格、材质等性能参数及矫直精度等要求，首先确定辊系型式为对辊六辊结构，然后确定辊距和立柱位置等结构参数，再进一步计算出矫直力。利用大型通用的有限元结构分析软件ANSYS，根据结构的实际尺寸，建成如图4所示的矫直机机架上横梁模型。

（2）对模型进行加载及约束

在上横梁模型（图4）中，分别在中间3个大圆筒的圆环面向上加载矫直力2500 kN，并分别将周边安装立柱的8个圆环面约束固定。在将上横梁边界条件及各参数设定后，开始利用ANSYS软件进行单元格划分及计算。

（3）模型分析

矫直机机架的上横梁受力情况如图5所示，可以看出横梁在额定载荷条件下，最大等效应力为75.66 MPa（压应力状态）；因此，立柱孔附近的应力集中状况可以不作强度分析的重点。另外，从矫直机机架上横梁内部筋板受力情况（图6）可以看出，横梁中的部分筋板存在应力集中的情况，也有部分筋板基本上处于不受力的状态，如图6中标记的1、2筋板。虽然在设计的时候，对主要受力的筋板采用了较厚的钢板，但其平均应力为35～42 MPa，横梁的屈服强度为250 MPa，因此安全系数仅为6.0～7.1。通常设计要求安全系数为8.0～10.0，可见横梁偏弱。

机架上横梁改进结构的模型及分析（1）结构改进

从上述的计算结果可以看出， 矫直机机架上横梁受力偏大，安全系数不够，因此需要改进。

① 加强筋板厚度。从图6中可以看出，筋板3为主要受力板，将此板加厚10 mm，重新分析计算，结果显示筋板3的受力稍微减小，但改善效果不明显。可以得出结论：不改变筋板布置、仅加强筋板厚度的办法对横梁的受力改善不大。

② 改变筋板布置。根据横梁的受力与约束条件可以看出，当正常工作时，3个矫直辊全部受力，横梁中间部分以立柱孔为固定点整体向受力方向弯曲，因而筋板3受力很大，筋板1、2几乎不受力。改进措施：在不改变横梁筋板厚度的前提下，将不受力的筋板与受力点或固定点连接起来，于是在筋板1与固定点（立柱筒）之间增加筋板、在筋板2与中间受力筒之间增加筋板， 模型如图6所示。重新分析计算，结果是内部各筋板均受力，且受力更均匀，应力减小明显。

（2）强度分析

在同样的材料属性和同样的边界条件下，对改进后的模型进行分析。

上横梁改进之后的模型筋板受力状况有了很大程度的改善，各个筋板得到充分利用，应力分布比较均匀。根据计算结果，筋板上的最大等效应力都在25～30 MPa之间，所以其安全系数为8.3～10.0，改进后的结构完全满足设计要求的安全系数。

机架上横梁改进前后性能对比对矫直机机架上横梁的筋板进行重新布置、优化后，在额定载荷条件下，其受力由原来的35～42MPa减小为25～30 MPa，强度性能大约提高了25%，并且受力分布也更加均匀。

上横梁的筋板进行重新布置、优化后，横梁在额定载荷条件下，最大位移由原来的0.339 mm变为0.276 mm，整体刚度提高了18.6%。

上横梁的筋板进行重新布置、优化后，横梁内部筋板的安全系数由原来的6.0～7.1提高到8.3～10.0，安全系数大大提高。3

本词条内容贡献者为:

张磊 - 副教授 - 西南大学