共轭复根是一对特殊根。指多项式或代数方程的一类成对出现的根。若非实复数α是实系数n次方程f(x)=0的根，则其共轭复数α*也是方程f(x)=0的根，且α与α*的重数相同，则称α与α*是该方程的一对共轭复（虚）根。1

共轭复根经常出现于一元二次方程中，若用公式法解得根的判别式小于零，则该方程的根为一对共轭复根。

定义方程两个互为共轭复数的根，称为方程的一对共轭复根。2

通常出现在一元二次方程中。若根的判别式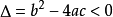 ，方程有一对共轭复根。

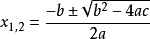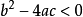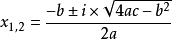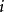根据一元二次方程求根公式韦达定理： ，当 时，方程无实根，但在复数范围内有2个复根。复根的求法为 （其中 是复数， ）。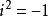

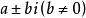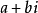由于共轭复数的定义是形如 的形式，称 与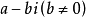 为共轭复数。

另一种表达方法可用向量法表达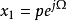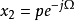： ， 。其中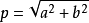 ，tanΩ=b/a。

由于一元二次方程的两根满足上述形式，故一元二次方程在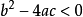 时的两根为共轭复根。

根与系数关系： ， 。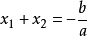

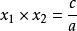应用常系数齐次线性微分方程如果3P(x)，Q(x)都是x的函数。方程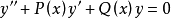的通解一般来讲是不容易求出的，当P(x)，Q(x)为常数时，微分方程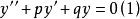的求解方法如下：

该方程称为二阶常系数齐次线性方程。当r为常数时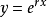，的各阶导数都只相差一个常数因子。设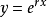，将其代入方程(1)，得：

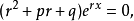
消去erx，得微分方程(1)的特征方程为：

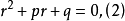
r是特征方程(2)的解的充要条件是erx是微分方程(1)的解。

若方程(2)有一对共轭的复根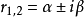时，方程(1)的通解为：

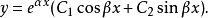
拉式反变换对线性系统4而言，响应的象函数F(s) 常具有有理分式的形式，它可以表示为两个实系数的s的多项式之比，即

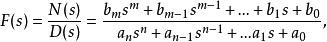
式中，m和n为正整数，若m 0，有2m对模长等于1的共轭复根（不等于1和-1），其余n−2m个根的模长都小于1，则的Jury阵中的元素之间满足：n=2m+1时下列条件①②③⑤⑥成立，n>2m+1时条件①②③④⑤⑥成立。

①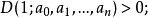

②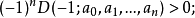

③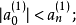

④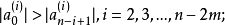

⑤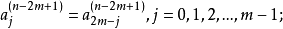

⑥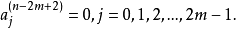

离散系统**引理5：**实系数多项式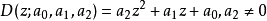的两个根是一对模长为1的共轭复根（不等于1和-1）的充要条件是：

①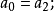

②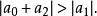

**定理：**实系数多项式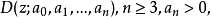有一对模长等于1的共轭复根（不等于1和-1），其余n-2个根的模长都小于1的充要条件是：n=3时下列条件①②③⑤成立；n>3时下列条件①②③④⑤成立：

①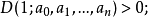

②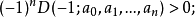

③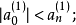

④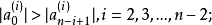

⑤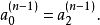

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学