若曲面上的一点P,其第一、二基本形式成比例,则称P点为曲面的脐****点(umbilical point)。若第二基本形式为零,则称为平点,否则称为圆点。在脐点处总曲率K=H2(H为平均曲率),两个主曲率相等,任何方向均为主方向。每点均为脐点的曲面(称为全脐点曲面)必为平面或球面1。
基本介绍脐点(umbilical point)是曲面上的一类特殊点,它是第一基本形式与第二基本形式成比例的点,若曲面在某一点处的第一、二类基本量适合
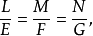 则称该点为曲面的脐点。曲面在脐点处的每一个切方向都是主方向,沿各方向的法曲率都相等,
则称该点为曲面的脐点。曲面在脐点处的每一个切方向都是主方向,沿各方向的法曲率都相等,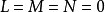 的脐点称为平点,
的脐点称为平点,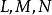 不全为零的脐点称为圆点,平面上的点都是平点,球面上的点都是圆点。
不全为零的脐点称为圆点,平面上的点都是平点,球面上的点都是圆点。
法曲率与脐点法曲率是曲面理论的一个核心概念。
设
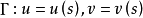 为曲面上任意曲线,s为弧长。法曲率为
为曲面上任意曲线,s为弧长。法曲率为
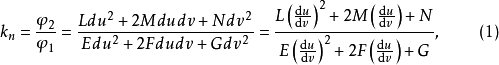 由于对任何方向,
由于对任何方向,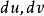 不能同时为零,故不妨在(1)中设
不能同时为零,故不妨在(1)中设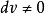 ,这表明法曲率是方向
,这表明法曲率是方向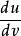 的函数,一般的说不同方向上
的函数,一般的说不同方向上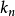 的值也不相同。所谓脐点,就是指曲面上这样一种特殊的点,它的任何方向的
的值也不相同。所谓脐点,就是指曲面上这样一种特殊的点,它的任何方向的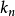 恒为常数。
恒为常数。
于是对于脐点,(1)式中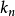 为常数,且对任何方向都成立,自然对于参数曲线方向亦成立,对
为常数,且对任何方向都成立,自然对于参数曲线方向亦成立,对 线显然有
线显然有
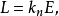 同样对v线有
同样对v线有
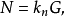 当
当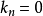 时,由上述两式可直接得到
时,由上述两式可直接得到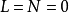 ,再代入(1)式便知
,再代入(1)式便知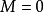 。至于
。至于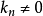 时,则将两式代入(1)式有
时,则将两式代入(1)式有
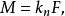 总之有
总之有
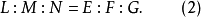
反之,若(2)式成立,则当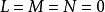 时,显然对任何方向均有
时,显然对任何方向均有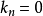 。若
。若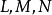 不全为零,不妨设
不全为零,不妨设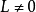 ,于是令
,于是令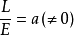 ,则有
,则有
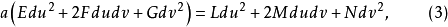 从而
从而
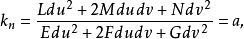 因对曲面上一定点,
因对曲面上一定点,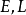 为定值,故
为定值,故 为常数。于是有:
为常数。于是有:
定理 曲面上一点为脐点的充要条件是
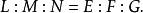
由上述定理的证明过程可以看到,平点是脐点中的一种。
我们又称L、M、N不全为零的脐点为圆点。球面上的点皆为圆点,而且可以证明其逆也成立,从而有:一个曲面为球面或球面一部分的充要条件是其上的每一点都是圆点。对于圆点,如上不妨令
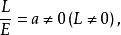 再根据(3)式以及
再根据(3)式以及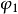 为恒正齐式,即得
为恒正齐式,即得
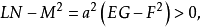 从而可知圆点是椭圆点的特殊情形2。
从而可知圆点是椭圆点的特殊情形2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

