定理内容

静电体系内存在电荷分布和电介质分布, 且关系式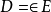 成立, 如给定电荷分布和电介质分布, 整个边界上给定下列件条之一或边界上所有各部分分别给定下列条件之一1

( 1 )电势 ,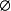

(2 )法线分量 , ·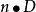

(3 电势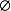 是一个未知常数，且电位移通量 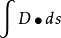=给定常数,

则体系的静电场被唯一确定。

由上面所给唯一性定理, 直接可得出下面两种形式的唯一性定理:

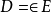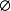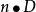( l) 静电体系内存在电荷分布和电介质分布且关系式 成立，则体系的电场由电荷和电介质分布, 边界上的 或 唯一确定。

( 2 ) 区域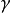 由封闭曲面: 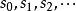等包围。如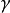 内电荷分布和电介质分布给定, 且关系式 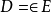成立, 若在各边界面上分别给定下列条件之一: ①s上电位给定, ②s上的电位移矢量的法线分量D 给定, ③ 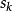为导体表面且总电荷给定. 则区域 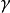内的电场被唯一确定.

以上唯一性定理对电介质分区均匀情况显然成立。

论证过程引理+叠加定理+证明2

引理一：在无电荷的空间里电势不可能有极大值和极小值。

引理二：若所有导体的的电势为0，则导体以外空间的电势处处为0。

引理三：若所有导体都不带电，则各导体的电势都相等。

叠加定理：在给定各带电导体的几何形状、相对位置后，赋予两组边界条件：

1）给定每个导体的电势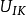 或总电量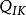

2)给定每个导体的电势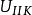 或总电量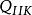

设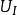 、 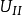满足上述两个条件，则他们的线性组合 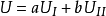必满足条件三

3)给定每个导体的电势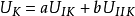或总电量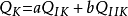

特例：取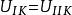,则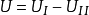(a=1,b=-1)

4)给定每个导体的电势为0

其中，引理二和引理三可推论：所有导体都不带电的情况下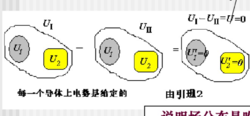，空间各处的电势和导体一样，等于同一个常量。

由上可推出唯一性定理，给定每个导体电势的情形，且设同一组边值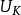（k=1,2,...）有两种恒定的电势分布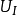和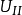，如下图过程，便可得到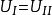即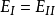,因此推得唯一性定理。

至于唯一性定理的证明过程可查阅郭硕鸿的《电动力学》，这里已经给出非常清晰的证明。

定理的应用静电场的唯一性定理可以用来直接或间接求解静电场，如常用的试探法、镜像法求解静电场，而其他求解静电场的常规方法如分离变量法和格林函数法，在求解静电场时以解析法直接解场方程的方式得到场解，似乎无需用到唯一性定理，但实际求解时，唯一性定理的应用解决了所得解的正确性和唯一性的问题。以下以典型的静电场求解问题为例阐明定理的应用和重要性静电场的唯一性定理可以用来直接或间接求解静电场，如常用的试探法、镜像法求解静电场，而其他求解静电场的常规方法如分离变量法和格林函数法，在求解静电场时以解析法直接解场方程的方式得到场解，似乎无需用到唯一性定理，但实际求解时，唯一性定理的应用解决了所得解的正确性和唯一性的问题。以下以典型的静电场求解问题为例阐明定理的应用和重要性。3

唯一性定理在镜像法中的应用镜像法是求解静电场边值问题较为直观的方法。在使用镜像法求解静电场时，镜像电荷的设置和场解的具体形式必须在满足唯一性定理的前提件下提出，即镜像电荷不能放置在待求场区，否则影响场方程，解的形式除了满足介质交界面上的衔接条件外，还要满足其他边界处的条件，这样才能保证场解是唯一正确的。故唯一性定理的应用是镜像法解题的核心思想之一。

唯一性定理在分离变量法中的应用分离变量法是较为严格的数学解析求解场方程的方法。

在使用分离变量法得到静电场场解的过程中，使用唯一性定理分析问题可以使解题思路明确，数学计算简化，场解的唯一正确性得到理论上的保证。在教学过程中，分离变量法较为严格的数学解析过程较容易为学生接受，故如果先由分离变量法开始，分析唯一性定理的应用思想，深入剖析问题的物理本质，进而尝试使用其他解法更容易令学生接受，在教学中会起到良好的效果。

唯一性定理直接求解静电场试探法是直接应用唯一性定理求解静电场的方法。

试探法在静电场边值问题中的应用直接体现了唯一性定理在求解静电场时的重要意义和价值。表现为当静电场的场方程和边界条件确定时，无论通过何种途径得到的解，只要满足场方程和边界条件，所得解必为唯一正确的解。分析如下: 1) 提出适当的尝试解的形式满足场方程; 2) 场解的具体形式由边界条件决定; 3) 无需严谨的数学推导，得到的场解必是唯一正确的。

唯一性定理解释静电屏蔽唯一性定理表明：一旦找到某种电荷分布既不违背导体平衡特性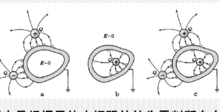，又是物理实在，则这种电荷分布就是唯一可能的分布。如右图所示。

关于此定理的应用需注意:1) 在满足唯一性定理的条件下，解是唯一的，但是不同情况下解的具体表述形式可以是不同的;

2) 区域的边界条件可以分为3 种，第1 类为Dirichlet 边界条件即给定边界电势; 第2 类为Neumann 边界条件即给定边界电势的法向导数; 第3 类为混合边界条件即已知一部分边界电势，已知一部分边界电势的法向导数。