简介

给定两个测度空间Ω1和Ω2，映射f：Ω1→Ω2称为从Ω1到Ω2的可测变换。是从一个测度空间到另一个测度空间之间的一个映射。设f是从Ω1到Ω2的可测变换，且f是双射，则称f为从Ω1到Ω2的双可测变换****。

概念可测变换亦称可测映射，是可测函数概念的推广，主要用于抽象积分的变数变换。设(Ω1，F1)和(Ω2，F2)是两个可测空间，f是Ω1到Ω2中的映射。如果(Ω2，F2)中每个可测集A的原像f-1(A)均是(Ω1，F1)中的可测集，那么f称为Ω1到Ω2的可测映射。若f是可测空间(Ω，F)上的实值函数，则f在(Ω，F)上可测的充分必要条件是f为(Ω，F)到(Rc，Bc)中的可测映射，其中R为实数空间，B为波莱尔集类。若f是可测空间(Ω，F)上的扩充实值函数，则f在(Ω，F)上可测的充分必要条件是f为(Ω，F)到(R，B)中的可测映射，其中R为扩充实数空间，B为广义波莱尔集类。若f是测度空间(Ω，F，μ)到可测空间(Ω′，C)的可测映射，g是(Ω′，C)上的可积函数，则：1

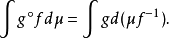又若A∈C，则：

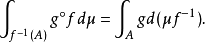
测度论亦称抽象测度论或抽象积分论，研究一般集合上的测度和积分的理论。是勒贝格测度和勒贝格积分理论的进一步抽象和发展。

测度是集合的一种度量，它是长度、面积、体积概念的推广。首先试图把长度、面积、体积概念推广到任意点集而得出一般的“测度”观念的是杜·布瓦-雷蒙( P.D.G.Du Bois-Reymond)，他在《一般函数论》(1882年)中提出容量概念，即测度概念的雏形。随后汉克尔(H.Hankel)、施托尔茨(O.Stolz)、哈纳克(C.G.A.Harnack)、康托尔(G.(F.P.).Cantor)等人发展了这种思想，其中康托尔于1884年对直线上的有界集A定义它的测度μ(A)：首先对任意正数δ，令：

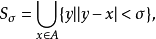μ(Sδ)代表Sδ的长度；再令：

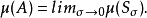康托尔给出的测度不具有可加性。例如，设Q为有理数全体，A=[0，1]∩Q，B=[0，1]\A，则[0，1]=A∪B，μ(A)=μ(B)=1，μ([0，1])=1，但μ([0，1])≠μ(A)+μ(B)，因而很不合理。

佩亚诺(G.Peano)于1887年引入了平面有界集A的内、外测度的概念：包含A的多边形面积的下确界称为A的外测度，含于A内的多边形面积的上确界称为A的内测度。若A的内、外测度相等，则这个公共值称为A的测度，并称A为可测集。佩亚诺证明了：

1.A可测的充分必要条件是A的边界的外测度为0。

2.若f(x)是定义在[a，b]上的有界正函数，A={(x，y)|a≤x≤b，0≤y≤f(x)}，则f(x)的黎曼下积分为A的内测度，黎曼上积分为A的外测度，f(x)黎曼可积当且仅当A是可测集。

3.测度具有有限可加性。

若尔当(M.E.C.Jordan，)于1892年在R中发展了佩亚诺可测集的概念。原来定义外测度时，要用多边形去覆盖点集，他规范为用有限个开区间去覆盖，其余不变.若尔当的改进使测度概念前进了一大步，蕴涵了勒贝格测度的萌芽，但仍有明显的缺点。主要是它仍只具有有限可加性，从而导致有些简单的点集也不可测。例如，令A=[0，1]∩Q，则A的若尔当内测度为0，而外测度为1，因而A在若尔当意义下不可测。总之，若尔当测度只适合于黎曼积分的需要。波莱尔((F.-É.-J.-)É.Borel)于1898年，先由开集经过可列并与余的运算导致一类集，即所谓波莱尔集类。再对每个有界波莱尔集对应一个实数，即波莱尔测度，并使得这种测度具有可列可加性。波莱尔的这种思想对测度理论做出了重大贡献，成为近代测度论中用公理方式引出σ代数概念的起源，并为勒贝格(H.L.Lebesgue)的工作开辟了道路。波莱尔的学生勒贝格在前人工作的基础上，于1902年以更一般的形式建立起比较完善的测度理论.他在定义点集测度的方法上，容许可列覆盖，使所建立的测度具有可列可加性，并且相当广泛的一类点集的测度有了定义。勒贝格测度是现代抽象测度的起源，在它的基础上建立的勒贝格积分，是现代分析中应用最广和意义重大的积分。卡拉西奥多里(C.Carathéodory)于1914年发展了外测度理论，对测度进行了公理化研究，并给出了测度扩张的典型方法，成为近代测度论的基础.拉东(J.Radon)、萨克斯(S.Saks)、弗雷歇(M.-R.Fréchet)以及另外一些人考虑了一般集合上的测度以及测度空间的乘积，并建立了一般可测集上积分的理论。

一般集合上的测度和积分理论是最广泛的测度理论，但为适应各方面的需要，还出现了其他种种特殊的测度和积分。例如，20世纪30年代初，伴随着人们对取值于巴拿赫空间的函数性质特别是可微性和可积性的研究，出现了有关向量值测度的一些工作。1960年以后，向量值测度理论得到蓬勃发展，并逐渐趋于完善。又如，19世纪建立的傅里叶分析理论，对于应用数学而言，当时已是令人满意的数学工具，但由于黎曼积分的局限性，对于函数与展开式之间的关系，直到勒贝格积分理论确立之后才有深刻的揭示.勒贝格积分的出现对于傅里叶展开的研究显然促进了一大步，但依旧显示出了它的局限性.研究拓扑群上的测度是建立群上傅里叶分析的基本问题之一，这个问题自1930年以来，经过哈尔(Haar，A.)、韦伊(A.Weil)和盖尔范德(И.М.Гельфанд)等人的工作而趋于完善.再如，20世纪初测度论的建立，使得人们对R中的子集关于n维勒贝格测度的性质有了很好的了解。但在处理与R中低维点集有关的数学问题时遇到了困难。在这种背景下，20世纪20年代出现了几何测度论，它是研究高维空间中低维点集的测度及低维点集上积分的理论。

测度概念与积分概念紧密相关。每一种测度理论的推广都可导致一种积分理论的推广。测度理论不仅是积分理论的基础，而且在现代分析以及概率论等许多数学领域中也有着广泛的应用。2

可测函数分析学中讨论得最广的函数类。它有许多等价的定义方式，这里采用如下定义：设(Ω，F)为可测空间，f(x)是定义在Ω上的实值(或扩充实值)函数。若对任意实数c，恒有{x|f(x)>c}∈F，则f(x)称为(Ω，F)中的可测函数或Ω上的F可测函数。在这个定义中，条件f(x)>c可用f(x)≥c，f(x)