设给定一数集E,若存在m R,使得对于
R,使得对于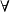 x
x E,都有x
E,都有x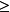 m,则称m是集合E的一个下界。1
m,则称m是集合E的一个下界。1
例:若E=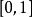 ,不难验证只要m
,不难验证只要m
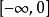 ,m就是集合E的一个下界。
,m就是集合E的一个下界。
一个数集可以由有限个数组成,也可以由无穷多个数组成,前者称为有限(数)集,后者称为无限(数)集。任何有限数集都有一个最小数,但对于无限数集来说就不一定有最小数了。例如,由一切x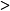 1所组成的数集没有最小数;又如数集
1所组成的数集没有最小数;又如数集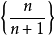 (
(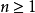 )有最小数1/2.2
)有最小数1/2.2
我们知道,有界数集有无穷多个下界。因而,对于有有界数集来说,如果它有最小数,那么这个最小数也是它的下界中的一个,并且比这个最小数大的任何数都不是它的下界,这时,这个最小数自然就是它的最大的下界。2
但在上面的例子中已经看到,对一般无限数集来讲不一定有最小数。然而,对于某些无限数集来说,最大的下界确实存在,这里暂时撇开最大下界的存在性,而对一般数集的最大下界给予确切的定义。2
设给定一数集E。若存在这样一个数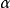 ,适合以下两个条件:
,适合以下两个条件:
(i)集E中的一切数x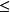
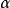 (即
(即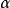 是E的一个下界);
是E的一个下界);
(ii)对任意给定的正数 ,至少存在一个数
,至少存在一个数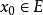 ,使得
,使得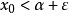 (即比
(即比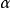 再大一点就不是下界), 则
再大一点就不是下界), 则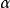 叫做E的下确界,记为
叫做E的下确界,记为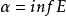 或
或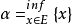 . 这里inf是infimum的缩写。
. 这里inf是infimum的缩写。
第一个条件说明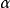 是E的下界之一,而第二个条件说明凡大于
是E的下界之一,而第二个条件说明凡大于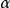 的任何数都不是E的下界。也就是说
的任何数都不是E的下界。也就是说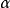 是E的最大下界。
是E的最大下界。
注1 为方便起见,若E无下界,则记 .
.
注2 上面的条件(ii)等价于:如果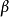 是E的一个下界,则必有
是E的一个下界,则必有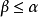 .1
.1
定理 设数集有上(下)确界,则这上(下)确界是唯一的。2
证明:采用反证法。假设数集E有两个不同下确界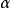 和
和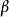 (
(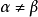 ),显然,
),显然,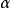 和
和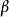 均为E的下界,由上面注2可知
均为E的下界,由上面注2可知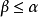 且
且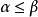 ,故
,故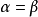 . 与假设相矛盾!证毕。
. 与假设相矛盾!证毕。
定理 有上界的非空数集必有上确界,有下界的非空数集必有下确界。2
证明3:用戴德金分割定理证明。
戴德金定理:对实数集R的任意一个满足不空、不漏、不乱的划分A和B,都存在唯一的一个分点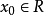 满足
满足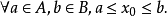
记给定非空集为X。取定B为X的所有上界的集合,A=R\B. 下证A、B为不空、不漏、不乱的划分。
不空:由于X非空,可取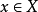 ,易知x-1不可能为X的上界,故A非空。B非空给定;
,易知x-1不可能为X的上界,故A非空。B非空给定;
不漏:由A=R\B知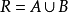 ;
;
不乱:设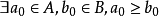 ,则由
,则由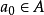 知
知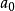 不是X的上界,即
不是X的上界,即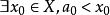 ,但又由
,但又由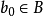 是X的上界知
是X的上界知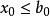 . 综上,
. 综上,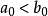 又
又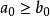 ,矛盾。不乱得证。
,矛盾。不乱得证。
故存在唯一的一个分点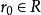 满足
满足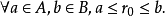 下证分点为上确界,即
下证分点为上确界,即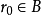 .
.
若不然,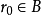 不成立,则
不成立,则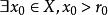 ,但此时就有
,但此时就有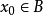 ,由
,由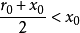 知
知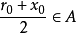 ,与
,与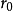 是划分A和B的分点相矛盾。故
是划分A和B的分点相矛盾。故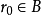 .
.
下确界同理。证毕。
3. 单调有界数列必有极限定理 单调有界数列必有极限。2
证明:我们只就单调减少的有界数列予以证明。设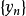 有界,则必有下确界
有界,则必有下确界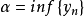 . 再设
. 再设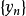 是单调减少的,现在证明
是单调减少的,现在证明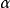 恰好就是
恰好就是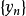 的极限,即
的极限,即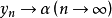 .
.
由下确界的定义有(i)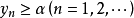 ;(ii)对任意给定的
;(ii)对任意给定的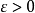 ,在
,在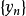 中至少有一数
中至少有一数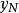 ,有
,有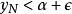 . 但由于
. 但由于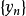 是单调减少数列,因此当
是单调减少数列,因此当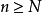 时,有
时,有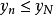 ,从而
,从而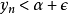 . 也就是说,当
. 也就是说,当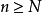 时,有
时,有
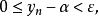 所以
所以
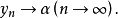
这里不仅证明了单调有界数列的极限存在,而且也证明了如果它是单调减少的,则极限就是它的下确界。同样可证单调增加有界数列的极限存在,并且极限就是它的上确界。


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

