定义

设G为群。对于G中共轭的两个元素a和b，必存在G中一个元素g，满足1

gag=b。

（在线性代数中，这叫做相似变换。）

很容易证明共轭是等价关系，因此将G分割为等价类。（这表示群的每个元素属于恰好一个共轭类，而类Cl(a)和Cl(b)相等当且仅当a和b共轭，否则不相交。）包含元素a属于G的等价类是

Cl(a) = {gag:g∈G}

并称为a的共轭类。G的类数是共轭类的个数。

例子对称群S3，由所有3个元素的6个置换组成，拥有三个共轭类：2

恒等 (abc -> abc)表示为(1)

对换 (abc -> acb，abc -> bac，abc -> cba)表示为(23) (12) (13)

三阶轮换 (abc -> bca，abc -> cab)表示为(132) (123)

对称群S4，由4个元素的全部24个置换组成，有5个共轭类：

恒等

对换

三阶轮换

四阶轮换

双对换

参看立方体的恰当转动，它可以用体对角线的枚举刻划。

在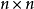矩阵，在同一个共轭类的矩阵称为相似矩阵。

属性单位元总是自成一类，也就是说Cl(e) = {e}

若G可交换，则gag=a对于所有a和g属于G成立；所以Cl(a) = {a}对于a属于G成立；可见这个概念对于交换群不是很有用。

若G的两个元素a和b属于同一个共轭类（也即，若它们共轭），则它们有同样的阶。更一般地讲，每个关于a的命题可以转换成关于b=gag的一个命题，因为映射φ(x) =gxg是一个G的自同构。

G的一个元素a位于G的中心Z(G)当且仅当其共轭类只有一个元素，a本身。更一般地讲，若CG(a)代表G中的a的中心化子，也即，有所有满足ga=ag的元素g组成的子群，则指数[G: CG(a)]等于a的共轭类中元素的个数。2

共轭类方程定义若G为有限群，则上节的内容，加上拉格朗日定理，可以得出如下结论：每个共轭类的元素个数整除G的阶。

进一步的有，对于任何群G，可以通过从G的每个元素个数大于1的共轭类中取出一个元素来定义一个代表集S= {xi}。则G是Z(G)和S的元素的共轭类Cl(xi)的不交并集。由此可以写出重要的类方程：

|G| = |Z(G)| + ∑i[G:Hi]

其中求和取遍对于每个S中的xi的Hi= CG(xi)。注意[G:Hi]是共轭类i的元素个数，一个|G|的大于1的除数。如果|G|的除数已知，则该方程经常用于获得关于共轭类或者中心的大小的信息。

例子考虑一个有限p-群G（也即，次数为p的群，其中p是一个素数而n> 0）。我们将证明：每个有限p-群有非平凡的中心。

因为G的任意子群的次数必须整除G的次数，所以每个Hi也是某个幂p。但是类方程要求|G| =p= |Z(G)| + ∑i(p)。因此我们可以看出p必须整除|Z(G)|，所以|Z(G)| > 1。

子群的共轭更一般的来讲，给定任意G的子集S（S不必是子群），我们定义一个G的子集T为S的共轭，当且仅当存在某个g属于G满足T=gSg。我们可以定义**Cl(S)**为所有共轭于S的子集T的集合。

一个常用的定理是，给定任意子集S，N(S)（S的正规化子）的指数等于Cl(S)的次数：

|Cl(S)| = [G: N(S)]

这是因为，如果g和h属于G，则gSg=hSh当且仅当gh属于N(S)，换句话说，当且仅当g和h属于N(S)的同一个陪集。

注意这个公式推广了前面关于共轭类元素的个数的定理（S= {a}的特殊情况）。

上述定理在讨论G的子群时尤其有用。子群可以由此分为等价类，两个子群属于同一类当且仅当它们共轭。共轭子群是同构的，但是同构子群未必共轭（例如，交换群可以有两个不同的互相同构的子群，但是它们不可能共轭）。

作为群作用如果对于任意两个G中的元素g和x定义

g.x=gxg

则我们有了一个G在G上的群作用。该作用的轨道就是共轭类，而给定元素的定点子群就是该元素的中心化子。

同样，我们可以定义一个在G的所有子群或者所有子集的集合上的G的群作用如下

g.S=gSg。