设函数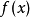 在区间
在区间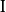 有定义,
有定义,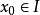 ,若
,若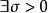 ,
,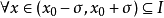 有
有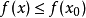 (或
(或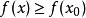 ),则称
),则称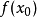 是函数
是函数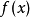 的一个极大值(或极小值),
的一个极大值(或极小值),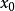 是函数
是函数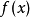 的一个极大值点(或极小值点)。极大值与极小值统称为极值;极大值点与极小值点统称为极值点。上面的不等号若严格成立,则称为严格极值点,对应函数值称为严格极值。1
的一个极大值点(或极小值点)。极大值与极小值统称为极值;极大值点与极小值点统称为极值点。上面的不等号若严格成立,则称为严格极值点,对应函数值称为严格极值。1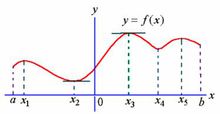
注意:
(1)极值点只关心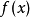 在
在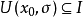 内的局部函数值,不关心是否可导。因此函数
内的局部函数值,不关心是否可导。因此函数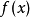 在极值点
在极值点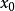 处可能不可导,如
处可能不可导,如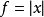 在
在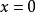 处不可导。
处不可导。
(2)极值点是函数图像的某段子区间内上极大值或者极小值点的横坐标。
(3)极值点出现在函数的驻点(导数为0的点)或不可导点处(导函数不存在,也可以取得极值,此时驻点不存在)。
(4)可导函数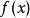 的极值点必定是它的驻点。但是反过来,函数的驻点却不一定是极值点,例如
的极值点必定是它的驻点。但是反过来,函数的驻点却不一定是极值点,例如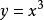 ,点
,点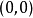 是它的驻点,却不是它的极值点。
是它的驻点,却不是它的极值点。
(5)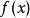 极值点上的导数为零或不存在,且函数的单调性必然变化。
极值点上的导数为零或不存在,且函数的单调性必然变化。
若函数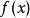 在
在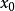 处可导,且
处可导,且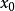 是函数
是函数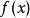 的极值点,则
的极值点,则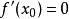
注:若去掉“函数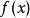 在
在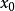 处可导”的条件,则函数
处可导”的条件,则函数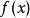 的极值点
的极值点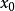 处不一定有
处不一定有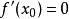 ,如
,如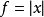 ;此外,若
;此外,若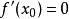 ,则
,则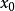 不一定是极值点,如
不一定是极值点,如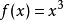 在
在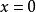 处,有
处,有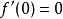 ,但
,但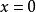 不是
不是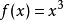 的极值点。1
的极值点。1
(1)若函数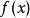 可导
可导
【第一判别法】若函数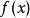 可导,
可导,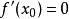 ,且
,且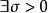 ,
,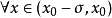 有
有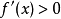 (或
(或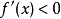 )同时,
)同时,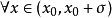 有
有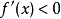 (或
(或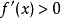 ),则
),则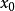 是函数
是函数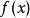 的极大点(或极小点)
的极大点(或极小点)
【第二判别法】若函数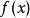 存在二阶导数,
存在二阶导数,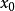 是函数
是函数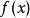 的稳定点,即
的稳定点,即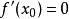 ,而
,而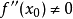 ,则当
,则当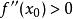 时,
时,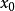 是函数
是函数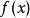 的极小点;当
的极小点;当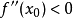 时,
时,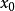 是函数
是函数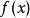 的极大点。
的极大点。
(2)若函数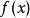 在一些点不可导,则需要用定义判断。1
在一些点不可导,则需要用定义判断。1
(1)单变量函数的极值求法
a. 求导数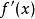 ;
;
b. 求方程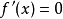 的根;
的根;
c. 检查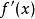 在函数图象左右的值的符号,如果左正右负,那么
在函数图象左右的值的符号,如果左正右负,那么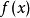 在这个根处取得极大值;如果左负右正,那么
在这个根处取得极大值;如果左负右正,那么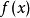 在这个根处取得极小值。
在这个根处取得极小值。
特别注意: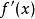 无意义的点也要讨论,即可先求出
无意义的点也要讨论,即可先求出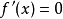 的根和
的根和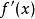 无意义的点,这些点都称为可疑点,再用定义去判断。 例如:
无意义的点,这些点都称为可疑点,再用定义去判断。 例如: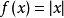 在
在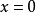 的导数是不存在的。
的导数是不存在的。
(2)二阶连续偏导数的函数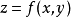 的极值求法,叙述如下:
的极值求法,叙述如下:
a. 解方程组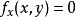 ,
,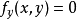 ,求得一切实数解,即可求得一切驻点;
,求得一切实数解,即可求得一切驻点;
b. 对于每一个驻点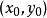 ,求出二阶偏导数的值
,求出二阶偏导数的值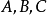 ;
;
c. 定出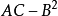 的符号,判定
的符号,判定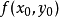 是否是极值,是极大值还是极小值。
是否是极值,是极大值还是极小值。
注意:当函数仅在区域D内的某些孤立点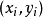 不可导时,这些点不是函数的驻点,但这种点有可能是函数的极值点,要注意另行讨论。
不可导时,这些点不是函数的驻点,但这种点有可能是函数的极值点,要注意另行讨论。
方程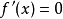 的解
的解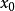 ,即
,即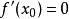 称为函数
称为函数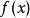 的稳定点
的稳定点
注:定义不要求函数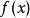 可导,所以可导函数
可导,所以可导函数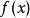 的极值点必须是稳定点,但稳定点不一定是极值点。1
的极值点必须是稳定点,但稳定点不一定是极值点。1


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

