定义
设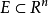 ,若对任意的点集
,若对任意的点集 ,有
,有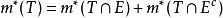 ,则称E为Lebesgue可测集,简称可测集。
,则称E为Lebesgue可测集,简称可测集。
注意事项如下:
(1)可测集的全体记为M,对于可测集E,称其外测度为测度,记为m(E)。
(2)称测度为零的可测集为零测集。空集、有限集、可数集皆为零测集。
(3)通常称定义中的条件为卡氏条件,称其中的集T为试验集。1
相关定理零集零集为可测集。2
证明:设E为零集,m*(E)=0,任意A⊂R,因为A∩E⊂E,所以有0≤m*(A∩E)≤m*(E),得m*(A∩E)=0,于是
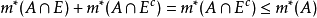
故E∈M。2
可测集的补集若E为可测集,则E的补集也是可测集。1
可测集的并集交集若A,B为可测集,则A∪B,A∩B,A\B皆为可测集。
证明:对任意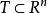 ,易得
,易得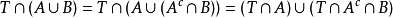 ,依次利用外测度的次可加性、B的可测性(取
,依次利用外测度的次可加性、B的可测性(取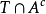 为试验集)以及A的可测性(取T为试验集),有:
为试验集)以及A的可测性(取T为试验集),有:
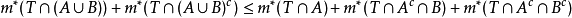
且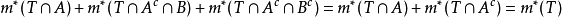
故得到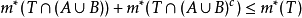 。
。
所以可知A∪B是可测集,从而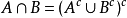 是可测集,A\B=
是可测集,A\B=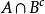 也是可测集。1
也是可测集。1
可数可加性若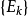 是互不相交的可测集列,则并集
是互不相交的可测集列,则并集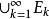 为可测集,且
为可测集,且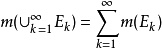 。
。
证明:对任意的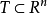 ,由外测度的次可加性等性质可知
,由外测度的次可加性等性质可知
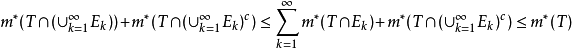
所以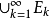 是可测集,令
是可测集,令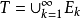 ,则有
,则有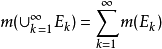 。1
。1
可测集列的交与并(1)若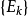 是可测集列,则并集
是可测集列,则并集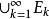 为可测集,且
为可测集,且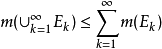 。1
。1
(2)若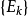 是可测集列,则交集
是可测集列,则交集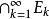 为可测集。1
为可测集。1
(3)若有递增可测集列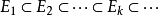 ,则
,则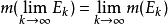 ,此时对可测集的极限有定义
,此时对可测集的极限有定义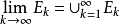 。1
。1
(4)若有递减可测集列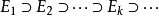 ,且
,且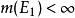 ,则
,则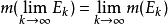 ,此时对可测集的极限有定义
,此时对可测集的极限有定义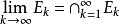 。1
。1
(5)任一可测集均可以表示为一列递增的有界可测集之并。3
(6)任一可测集均可以表示为一列两两不交的有界可测集之并。3
可测集类第一类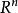 中的矩体是可测集。
中的矩体是可测集。
证明:设矩体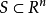 ,对任意矩体
,对任意矩体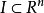 ,不妨设
,不妨设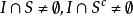 。记矩体
。记矩体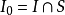 ,把
,把 分割成有限个互不相交的矩体之并:
分割成有限个互不相交的矩体之并: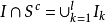 ,则有
,则有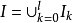 ,从而得到
,从而得到
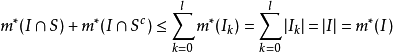
此时易得,矩体S为可测集。1
第二类由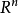 中开集的构造可知,每个开集可写成可列个互不相交的半开半闭的矩体之并,故开集必为可测的。由此易得到如下结论:
中开集的构造可知,每个开集可写成可列个互不相交的半开半闭的矩体之并,故开集必为可测的。由此易得到如下结论:
开集、闭集、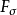 集、
集、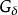 集、Borel集皆为可测集。1
集、Borel集皆为可测集。1
可测集的等价刻画设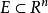 ,则下列条件等价:
,则下列条件等价:
(1)E是可测集;
(2)对任意ε>0,存在开集G⊃E,使m*(G\E)0,存在闭集F⊂E,使m*(E\F)


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

