二项式定理
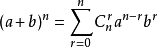
其中,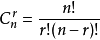 ,又有
,又有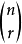 等记法,称为二项式系数,此系数亦可表示为杨辉三角形。等式的右边
等记法,称为二项式系数,此系数亦可表示为杨辉三角形。等式的右边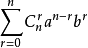 即为
即为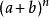 的展开式,称为二项展开式。
的展开式,称为二项展开式。
理解将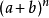 看成
看成 个
个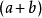 相乘,从每个括号中取一项 (非
相乘,从每个括号中取一项 (非 即
即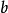 ) 相乘的所有单项式合并同类项得到的,按取
) 相乘的所有单项式合并同类项得到的,按取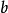 的个数分为
的个数分为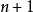 类 ,不取
类 ,不取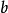 的是
的是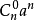 ,取 1 个
,取 1 个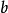 的是
的是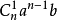 ,..., 取
,..., 取 个
个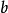 的是
的是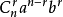 ,...,取
,...,取 个
个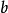 的是
的是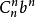
注意:1
(1)选取性,二项式的两项怎样选取 (各取几个) 才能构成所求的项;
(2)有序性,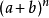 的展 开式第
的展 开式第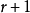 项是取
项是取 个
个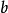 (同时取
(同时取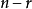 个
个 ), 这里的
), 这里的 和
和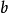 不能互换
不能互换
(3)项 、项的系数与二项式系数的区别
某项要把这一项全部写出来;某项的系数只写这一项的系数,不带字母 (即把每个字母当作数 1) ;某项的二项式系数就是相应的组合数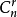
性质(1)项数:n+1项
(2)第k+1项的二项式系数是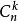
(3)在二项展开式中,与首末两端等距离的两项的二项式系数相等。
(4)如果二项式的幂指数是偶数,中间的一项的二项式系数最大。如果二项式的幂指数是奇数,中间两项的的二项式系数最大,并且相等。
(5)二项式通项: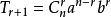 ,是第
,是第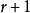 项
项
证明这里,采用数学归纳法对二项式定理进行证明
当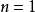 ,
,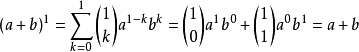
假设二项展开式在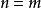 时成立,设
时成立,设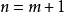 ,则:
,则:
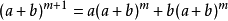
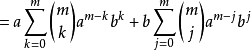
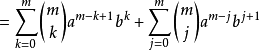
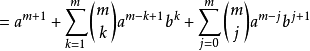 (取出
(取出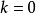 的项)
的项)
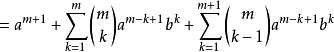 (设
(设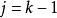 )
)
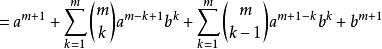 ( 取出
( 取出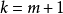 项)
项)
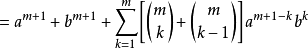 (两者相加)
(两者相加)
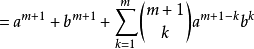 (套用帕斯卡法则)
(套用帕斯卡法则)
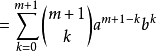
等式也成立
结论:对于任意自然数n,等式均成立。
例题某项的系数求二项展开式的某项或某项的系数是高考数学的一个基本知识点,每年的高考题都有一定的题出现。1
例1. 求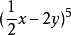 的展开式中
的展开式中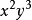 的系数
的系数
解: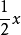 要取2个,故
要取2个,故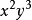 的系数是
的系数是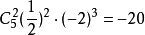
例2. 求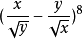 的展开式中
的展开式中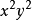 的系数
的系数
解: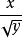 要取4个,故
要取4个,故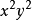 的系数是
的系数是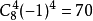
系数最值项例. 求 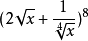 展开式中系数最大项和最小项2
展开式中系数最大项和最小项2
解:
通项=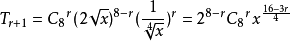
通项的系数=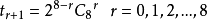
设系数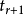 最大,则
最大,则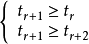
解得: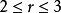 ,因为
,因为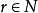 ,所以
,所以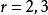 ,故系数最大项为
,故系数最大项为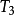 和
和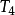
由于最大项在中间取得,所以最小项在两端,计算得: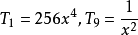 ,故系数最小项为
,故系数最小项为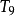
指定项求二项展开式中的指定项,一般是利用通项公式进行。3
例.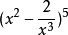 展开式中的常数项
展开式中的常数项
解:展开式的通项=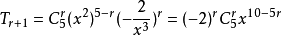 ,令
,令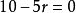 ,解得
,解得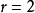
故常数项为: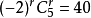


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

