定义
酉算子又叫保范算子,它是欧式空间中旋转概念在无穷维情况下的推广;希尔伯特空间的酉算子是仍保持其内积意义的希尔伯特空间的线性变换。酉算子具有逆算子,其逆算子也是一种酉算子,且酉算子和其逆算子是一对共轭算子。酉变换是泛函分析和算子理论中的一个重要概念,傅里叶变换就是酉变换之一例。1
设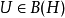 ,若满足:
,若满足:
(1)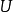 是等距的,即对任意
是等距的,即对任意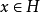 ,都有
,都有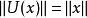 ;
;
(2)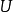 是满射。
是满射。
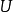 则称为酉算子。2
则称为酉算子。2
各种条件充要条件设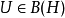 ,则
,则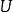 为酉算子等价于:
为酉算子等价于:
(1)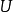 是满射且对任意
是满射且对任意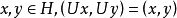 ;
;
(2)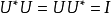 ,即
,即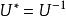 。
。
证明:
(1)充分性显然成立,下面证明必要性。
设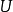 为酉算子,即
为酉算子,即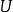 是满射且等距的,对任意
是满射且等距的,对任意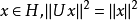 ,由极化恒等式得到下述等式:
,由极化恒等式得到下述等式:
当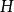 是实空间时,有:
是实空间时,有:
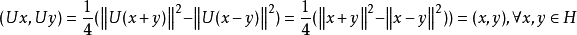
当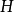 是复空间时,有:
是复空间时,有:
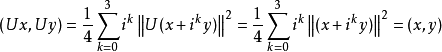
故有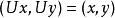 。
。
(2)首先来证必要性。
设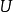 为酉算子,由(1)得,对任意的
为酉算子,由(1)得,对任意的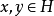 ,有:
,有: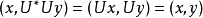 ,
,
所以得: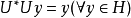 ;
;
故有: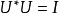 。
。
因此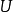 是单射,因而
是单射,因而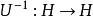 存在,且有:
存在,且有: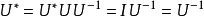 。
。
下面来证充分性。
由等式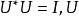 为满射,且对
为满射,且对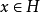 ,有:
,有:
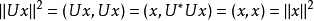
故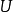 为酉算子。证毕。2
为酉算子。证毕。2
必要条件设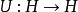 为酉算子,则
为酉算子,则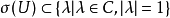 ,即酉算子的谱都在单位圆上。2
,即酉算子的谱都在单位圆上。2
酉算子的等价形式预备知识在复变函数中,保角映射在理论和应用上都十分重要,而具有保角性和伸缩率不变性的映射即为保角映射,将此概念推广到无穷维空间,特给出如下定义:
设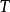 为线性算子,
为线性算子,
(1)若算子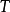 满足
满足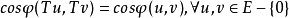 ,则称算子
,则称算子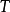 为保角算子;
为保角算子;
(2)若算子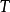 满足
满足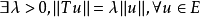 ,则称算子
,则称算子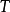 为相似算子;
为相似算子;
(3)若算子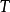 满足
满足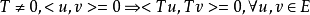 ,则称算子
,则称算子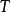 为第一型保正交算子;
为第一型保正交算子;
(4)若算子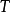 满足
满足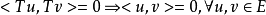 ,则称算子
,则称算子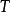 为第二型保正交算子;
为第二型保正交算子;
(5)若算子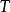 满足
满足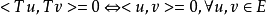 ,则称算子
,则称算子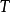 为正交不变算子;
为正交不变算子;
(6)若算子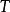 满足
满足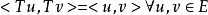 ,则称算子
,则称算子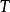 为酉算子,或保内积算子。3
为酉算子,或保内积算子。3
定理内容设为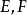 Hilbert空间,
Hilbert空间,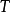 为由
为由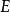 到
到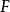 的线性算子,则关于算子
的线性算子,则关于算子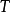 的如下六个命题为等价命题:
的如下六个命题为等价命题:
(1)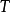 为保角算子;
为保角算子;
(2) 为相似算子;
为相似算子;
(3)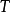 为第一型保正交算子;
为第一型保正交算子;
(4) 为第二型保正交算子;
为第二型保正交算子;
(5)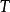 为正交不变算子;
为正交不变算子;
(6)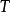 为酉算子。3
为酉算子。3


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

