全微分方程,又称恰当方程。若存在一个二元函数u(x,y)使得方程M(x,y)dx+N(x,y)dy=0的左端为全微分,即M(x,y)dx+N(x,y)dy=du(x,y),则称其为全微分方程。全微分方程的充分必要条件为∂M/∂y=∂N/∂x。为了求出全微分方程的原函数,可以采用不定积分法和分组法,对于不是全微分方程,也可以借助积分因子使其成为全微分方程,再通过以上方法求解。
定义一阶显式方程
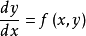 可以改写成关于
可以改写成关于 和
和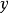 的对称形式
的对称形式
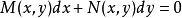 (1)
(1)
这种形式有时便于求解。这里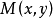 和
和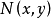 在某一矩形域
在某一矩形域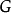 内是
内是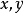 的连续函数,且具有连续的一阶偏导数。
的连续函数,且具有连续的一阶偏导数。
如果存在一个二元函数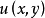 使得该方程的左端恰好是它的全微分,即有
使得该方程的左端恰好是它的全微分,即有
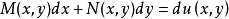 则称其为全微分方程(或恰当方程),而函数
则称其为全微分方程(或恰当方程),而函数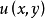 是
是 的原函数。1
的原函数。1
全微分方程的通积分形式当方程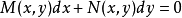 是全微分方程时,它可写成
是全微分方程时,它可写成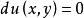 ,于是其通积分就是
,于是其通积分就是
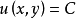 (2)
(2)
其中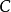 为任意常数。
为任意常数。
事实上,设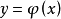 是原方程的解,则有
是原方程的解,则有
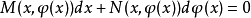 即有
即有
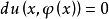 对
对 积分得到
积分得到
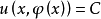
这表明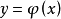 满足方程(2)。
满足方程(2)。
反之,设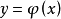 是函数方程(2)的解,即它是由(2)所确定的隐函数,则有
是函数方程(2)的解,即它是由(2)所确定的隐函数,则有
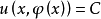 对
对 微分得到
微分得到
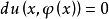
即
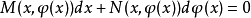
这表明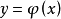 满足方程(1)。
满足方程(1)。
因此全微分方程的通积分形式是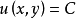 。
。
根据上述表述,为了求解方程(1),只要求出 的一个原函数
的一个原函数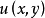 ,就可得到方程(1)的通积分(2)。1
,就可得到方程(1)的通积分(2)。1
全微分方程的判别与求解①如何判别方程(1)为全微分方程,这个问题在数学内早有结论,即
方程(1)是全微分方程的充分必要条件是
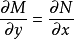 在矩形域
在矩形域 内成立。1
内成立。1
②如果已判定方程(1)为全微分方程,如何求出相应全微分的原函数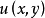 ,这个问题在数学分析中也已经得到解决,最常用的方法是不定积分法。
,这个问题在数学分析中也已经得到解决,最常用的方法是不定积分法。
因为所求的原函数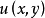 适应方程组
适应方程组
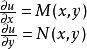
首先由第一个式子出发,把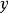 看成参数,两边对
看成参数,两边对 积分,得
积分,得
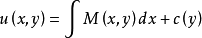 其中
其中 是
是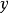 的任意可微函数,而且要选择适当的
的任意可微函数,而且要选择适当的 ,使
,使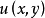 满足第二个式子。为此,将其代入第二个等式得
满足第二个式子。为此,将其代入第二个等式得
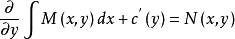 即
即
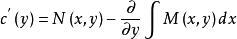 两边对
两边对 积分,即可得到
积分,即可得到 ,再代回之前的积分,即可得到
,再代回之前的积分,即可得到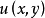 。
。
但对于某些特殊的全微分方程,为了求出相应全微分的原函数,还可以采用相对简单的“分组凑全微分”的方法,即把方程的左端各项进行重新组合,使每个组的原函数容易观察得出,从而可以写出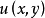 。1
。1
而对于不是全微分的方程,可以采用积分因子使其成为全微分方程,再根据以上方法求解。
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

