定义

不可约矩阵和可约矩阵（reducible matrix）两个相对的概念。

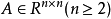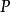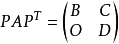表述一设 ，若存在置换矩阵 ，使得 ，其中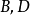 是阶数不小于1的方阵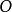， 是零矩阵，则称 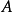是可约的；否则称矩阵 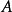是不可约的。1

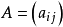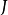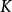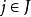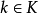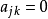表述二对于 阶方阵 而言，如果指标集 {1，2，...，n} 能够被划分成两个不相交的非空指标集 和 ，使得对任意的 和任意的 都有 ，则称矩阵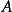 是可约的；否则称矩阵 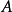是不可约的。

可约矩阵和不可约矩阵实例可约矩阵

其中A矩阵其对应的有向图并非强连通，故这个矩阵是可约的，其对应有向图如下所示：

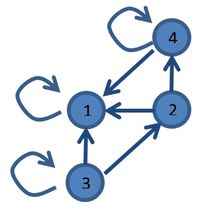
不可约矩阵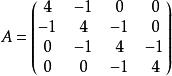

相关定理定理1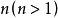 阶复数方阵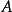 是不可约的当且仅当与矩阵 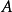对应的有向图 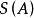是强连通的。2

说明：不可约矩阵不能分解成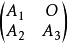 的形式，其中 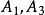为方阵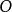， 为零矩阵。该定理的证明是显然的，不可约矩阵的么的任意次幂总是不可约的，因此它的右上角有一个零块。这个零块表明在 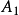所对应的顶点与 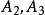所对应的顶点之间无通路。反之，如果一个有向图不是强连通的，则有一个不可达的顶点所对应的子块，经过适当的置换之后，对应的矩阵可以化为上面提到的形式。2

定理2一个方阵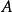 或者是不可约的，或者可以通过置换化为这样的规范形式：

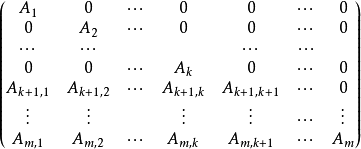
式中对角线上的子块是不可约阵。矩阵中出现对下标子块的任意一行至少有一个非零子块。2

说明：为证明这一定理，假定矩阵是可约的，因而它可以表示为可约矩阵定义的那种形式。如果对角线上的予块仍是可约的，这些子块又可以表示为那种定义形式。因此，只要对角线上的子块是可约的，总可表示为定义形式。经过适当地置换之后，主对角线上方的子块全部为零，对角线上的子块是不可约的。然后对于主对角线上的子块是唯一非零子块的那些行进行适当置换即可得到上述规范形式。2

注意到在图论的意义上，每个孤立的子块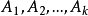从双下标所对应的结点是可达的，反之则不然。上述矩阵中每一列的所有双下标子阵可以简单写成一行子块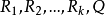，这里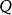不再是不可约的。若不考虑子块指标的置换，这种形式是唯一的。2

最后我们考虑矩阵的转置，子块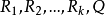构成矩阵的最后一列。事实上这是我们以后要用到的一种形式，即所谓排序的随机矩阵。排序的随机矩阵正规形式的构造可先从任意一个元素开始，在它所在的列中填写对这个元素有影响作用的所有元素的排序权值（即特征向量的分量）。然后再进行下一列，直到对这组元素全部填写完毕为止，必须逐元素地进行填写工作。对每一个不可约子集可得一个子块，填写完一块之后再填写下一块。2

定理3（1）当且仅当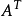不可约时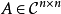，是不可约的；

（2）若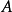是不可约的非负矩阵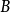，为非负矩阵，则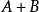是不可约矩阵。

证明：

对（1）是显然成立的。

对（2）采取反证法。若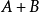是可约的，则存在置换矩阵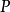使得：

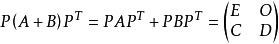
由于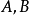都是非负矩阵，故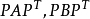都必须具有上式右端的形式，这与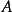是不可约的相互矛盾。3