定义
设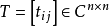 ,如果
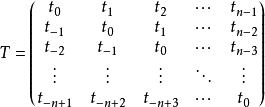
,如果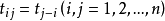 ,即:
,即:
则称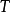 为托普利兹矩阵(Toeplitz matrix)。1
为托普利兹矩阵(Toeplitz matrix)。1
特点元素特点(1)托普利兹矩阵完全由其第1行和第1列的2n一1个元素确定。1
(2)托普利兹矩阵沿平行主对角线的每一对角线上的元素是相等的,是关于交叉对角线对称的。显然,有: ,其中
,其中 为反向单位矩阵。2
为反向单位矩阵。2
(3)除第一行第一列外,其他每个元素都与左上角的元素相同。3
(4)矩阵中的各元素关于次对角线对称,即T型矩阵为次对称矩阵。3
特殊的T形矩阵在数字信号处理领域中经常遇到一种特殊的T型矩阵,它除了具有一般T型矩阵的特点外,还是一个对称矩阵,3形式如下:

简单的T形矩阵前向移位矩阵
后向移位矩阵
相关定理定理1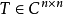 为托普利兹矩阵的充分必要条件是
为托普利兹矩阵的充分必要条件是 可以表示为:
可以表示为: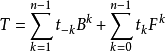 ,其中
,其中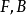 为前向位移矩阵和后向位移矩阵。1
为前向位移矩阵和后向位移矩阵。1
定理2非奇异矩阵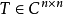 为托普利兹矩阵的充分必要条件是存在
为托普利兹矩阵的充分必要条件是存在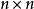 阶矩阵:
阶矩阵:
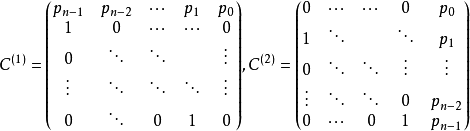
使得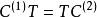 。1
。1
定理3若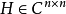 是汉克矩阵,则
是汉克矩阵,则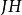 和
和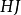 是托普利兹矩阵,其中
是托普利兹矩阵,其中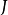 是反向单位矩阵;
是反向单位矩阵;
若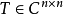 是托普利兹矩阵,则
是托普利兹矩阵,则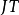 和
和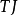 是汉克矩阵,其中
是汉克矩阵,其中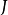 是反向单位矩阵。1
是反向单位矩阵。1
在MATLAB中生成托普利兹矩阵语法说明在数学软件Matlab中,生成托普利兹矩阵的函数是:toeplitz()。
(1)toeplitz(c,r),生成一个非对称的托普利兹矩阵,将c作为第1列,将r作为第1行,其余元素与左上角相邻元素相等。4
toeplitz(r)用向量r生成一个对称的托普利兹矩阵。4
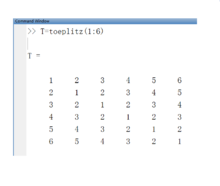
具体操作及结果例如,在MTLAB命令窗口中输入:T=toeplitz(1:6),结果如下:


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

