定义

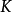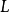设L是一个域。如果 是 的一个子集在域L中的加法与乘法运算封闭且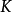中每个元素的加法与乘法逆仍在 中，则我们说 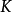是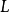 的一个子域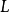， 看作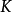上的扩域，叫做 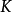上的域扩张，记作 。

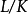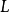的包含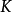 的任一子域叫做域扩张的一个中间域（或中间扩张或子扩张）。

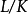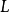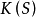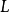给定一个域扩张 以及 的一个子集S，我们记为 包含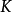 与的最小子域。我们说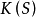由将S中元素添加到 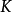中生成。如果S只包含一个元素s，我们通常记成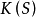。这样形式的域扩张称为单扩张，而s称为这个扩张的本原元。

给定一个域扩张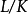 ，则L也可视为 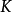上一个矢量空间。 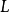中的元素是矢量而K中的元素是数量。矢量加法就是 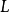中加法，数量乘法是用 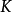中的元素乘以L中的元素。这个矢量空间的维数称为扩张的度数，记作。

度数1的扩张（即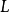 等于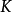 ）称为平凡扩张。度数为2和3的扩张分别称为二次扩张与三次扩张。由度数是有限或无限决定一个扩张称为有限扩张或无限扩张1。

基本性质如果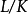 是一个域扩张，则 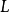和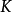 有相同的0和1。加法群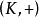是的一个子群，乘法群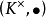 是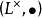 的一个子群。特别地，如果是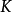 的一个元素，则在 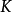中的加法逆−x与在 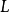中的加法逆相同；同样对K中非零元素的乘法逆也成立。特别地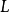， 与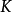 的特征相同。

设有域扩张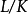 及某个中间域F，则域扩张 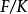和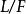 的次数乘积等于 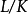的次数：

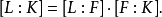
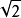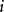代数元与超越元给定域扩张L/K，如果L中一个元素a是某个以K中元素为系数的（非零）多项式（以下简称为K-多项式）的根，则称a是K上的一个代数元，否则称其为超越元。如果L中每个元素都是K上的代数元，就称域扩张L/K为代数扩张，否则称其为超越扩张。例如 和 都是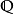 上的代数元，而e与π都是 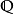上的超越元。 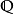上的代数元和超越元分别叫做代数数与超越数。

每个有限扩张都是代数扩张，反之则不然。超越扩张必然是无限扩张。给定域扩张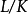 ，如果L中元素要么属于K，要么是K上的超越元，则称L是K的纯超越扩张。一个单扩张如果由添加代数元生成则是有限扩张，如果由添加超越元生成则是纯超越扩张2。

例子复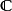数域 是实数域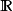 的扩域，而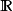 则是有理数域 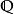的扩域。这样，显然 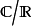也是一个域扩张。实数到复数的域扩张次数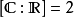： 。因为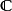 可以看作是以 为基的实向量空间。故扩张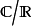 是有限扩张。 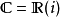，所以这个扩张是单扩张。

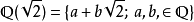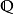集合 是在 中添加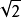 生成的扩域，显然也是一个单扩张。它的次数是2，因为 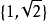可作为一个基。 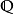的有限扩张也称为代数数域，在代数数论有重要地位。

有理数的另一个扩张域是关于一个素数p的p进数域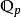 。它与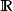 类似，是有理数域完备化得到的数域。但由于使用的拓扑不同，所以与 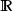有着截然不同的性质。

对任何的素数p和正整数n，都存在一个元素个数为p的有限域，记作GF(p)。它是有限域GF(p)（即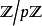 ）的扩域。

给定域K和以K中元素为系数的K-不可约多项式P，P为K上的多项式环K[X]的元素。P生成的理想是极大理想，因此K[X]/P是域，而且是K的扩域。其中不定元X是多项式P的根。

给定域K，考虑所有以K中元素为系数的有理函数，即可以表示为两个以K中元素为系数的多项式P、Q之比：PQ的函数。它们构成一个域，记作K(X)，是多项式环K[X]的分式域。它是域K的扩域，次数为无限大

正规、可分与伽罗瓦扩张伽罗瓦扩张是伽罗瓦理论中的基础概念。有限的伽罗瓦扩张满足伽罗瓦理论基本定理，在此扩张的伽罗瓦群的子群与其中间域之间建立了一一对应的关系，从而给出了中间域的清晰描述。

一般定义伽罗瓦扩张是正规且可分的域扩张。一个域扩张L/K称为正规扩张，如果对任何一个以K中元素为系数的不可约多项式P，只要它有一个根在L中，则它的所有根都在L中，也就是说可以分解为L上一次因式的乘积。正规扩张也叫做准伽罗瓦扩张，它与伽罗瓦扩张的差别是伽罗瓦扩张还是可分扩张。一个代数扩张L/K称为可分扩张，如果L中每个元素在K上的极小多项式是可分的，即（在K的一个代数闭包中）没有重根。从以上正规扩张和可分扩张的定义中可以推出：一个域扩张L/K是伽罗瓦扩张，当且仅当它是某个以K中元素为系数的可分多项式的分裂域。

伽罗瓦扩张的自同构群称为其伽罗瓦群，记作Gal(L/K)。它的阶数（群中元素个数）等于伽罗瓦扩张的次数：[L:K]= | Gal(L/K) |。伽罗瓦理论基本定理说明，当伽罗瓦扩张是有限扩张的时候，给定Gal(L/K)的任一个子群H，唯一存在一个中间域K⊂L⊂L与之对应，这个域L恰好是L中对所有的H中的自同构固定的元素的集合：

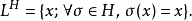这种对应关系被称作伽罗瓦对应。给定Gal(L/K)的子群H，L被称为H的对应域。伽罗瓦对应建立了特定条件下域扩张与群论之间转化的纽带，通过研究特定群的结构，可以给出域扩张的仔细刻画。

注释记号L/K纯粹是形式的，不表示商环或商群，或其他任何形式的除法。在某些文献中使用记号L:K。

经常希望在较小的域不是包含在较大的域中但是自然嵌入时谈论域扩张。为此，抽象地定义域扩张为两个域之间的一个单环同态。域之间的任何环同态是单射，故域扩张正好是域范畴中的态射。

在上面的讨论中，忽略单同态，处理的是真正的子域。