定义
设R为非空集合A上的偏序关系,如果任意的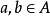 ,都有
,都有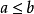 或
或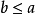 ,则称R为A上的全序关系(或线序关系),且
,则称R为A上的全序关系(或线序关系),且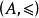 构成一个全序集或链。
构成一个全序集或链。
由定义可以知道,全序集的哈斯图是一条直线段2。
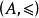
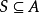
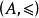 任一偏序集,若任意且S中存在最小元,则称为良序集。
任一偏序集,若任意且S中存在最小元,则称为良序集。
若两个全序集的元素相同,并且序关系也相同,则称这两个全序集是相同的,即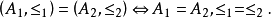 当用列举法表示全序集时,通常规定从左到右表示元素的顺序。例如,设N为自然数集,关系“≤”为平常的数的小于或等于关系,则全序集
当用列举法表示全序集时,通常规定从左到右表示元素的顺序。例如,设N为自然数集,关系“≤”为平常的数的小于或等于关系,则全序集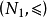 表示为
表示为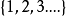 ;若序关系“
;若序关系“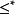 ”定义为
”定义为
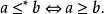
则全序集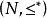 表示为
表示为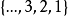 。1
。1
良序集与全序集定理1每一个良序集一定是全序集2。
注意:全序集不一定是良序集。
证明: 设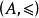 是良序集,则对于任意的
是良序集,则对于任意的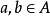 构成的子集一定存在最小元,该最小元不是a就是b,因此一定满足
构成的子集一定存在最小元,该最小元不是a就是b,因此一定满足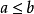 或
或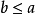 ,所以
,所以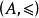 是全序集。
是全序集。
定理2任一个有限的全序集一定是良序集。
证明:设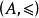 是任一有限全序集,
是任一有限全序集, 为任一非空子集,则B也是全序集。设B中有n个元素,将B中的元素依次进行比较,找出最小的那个元素,则最多进行
为任一非空子集,则B也是全序集。设B中有n个元素,将B中的元素依次进行比较,找出最小的那个元素,则最多进行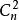 次比较,即
次比较,即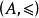 可找出最小元,因此是良序。
可找出最小元,因此是良序。
例题解析例1 给定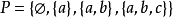 上的包含关系
上的包含关系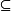 ,则
,则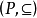 构成全序集。2
构成全序集。2
例2 给定自然数集N上的小于等于(≤)关系,则 构成全序集。
构成全序集。
例3 给定自然数集N上的小于等于(≤)关系,则 是良序集合。
是良序集合。
例4 给定整数集Z上的小于等于(≤)关系,则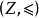 构成全序集。但因为在整数集上不存在最小元,所以该偏序集不是良序集。
构成全序集。但因为在整数集上不存在最小元,所以该偏序集不是良序集。
常见全序集1、 自然数集 、有理数集
、有理数集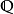 、实数集
、实数集 在通常的大小序下是全序的。
在通常的大小序下是全序的。
2、 有限长度的序列按字典序是全序的。最常见的是单词在字典中是全序的。
3、 任何良序集是全序的。
4、 自然数的子集按集合包含关系是一个偏序,但不是全序的,即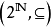 不是全序的。因为
不是全序的。因为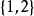 与
与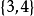 是不可比较的。
是不可比较的。


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

