定义

定义一

设M和N是巴拿赫微分流形,f∈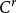 (M,N),W是N的 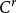子流形(r≥1).设p∈ 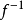(W), f(p)=q. 若复合映射

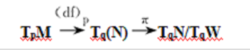
为满射且核裂,其中n为到商空间的自然投影,则称f在点p与W横截,记为f⫚pW. 如果对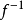 (W)中的每点p,均有f⫚pW,则称f与W横截,记为f⫚W.特别地,当 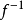(W)=∅时,也有f⫚W. 设q∈N,则f⫚{q}等价于q是f的正则值.设W1与W2是N的两个子流形,i1:W1→N为包含映射,若i1⫚W2,则称W1与W2横截.设M1,M2,N为 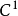流形,f2∈ 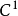(M2,N),若映射

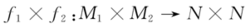
与N×N中的对角线流形Δ={(q,q)|q∈N}横截,则称映射f1与f2横截.下述原像定理反映了横截概念的重要性:

设f∈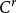 (M,N), W是N的 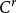子流形.若f⫚W,则当 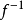(W)≠∅时, 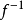(W)是M的 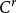(正则)子流形,且 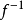(W)在M中的余维数等于W在N中的余维数.特别地,若q是f的正则值,且 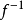(q)≠∅,则 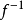(q)是M的 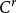子流形.1

定义二

设S⊂N是一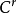 子流形，f：M→N为 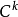映射，k，r≥1。我们说f在点p∈M横截于S，若f(p)∉S或

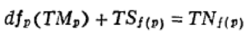
成立，即TMp在dfp下的像包含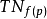 的互补于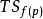 的一个子空间。如果f在每一点p∈M均与S横截，就称f与S横截，记作f⫚S。注意到若M的维数小于S的余维数，那么f与S是横截的当且仅当f(M)∩S=Φ。2

相关命题和推论命题1 映射f：M→N在点p∈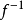 (S)与S横截当且仅当0是

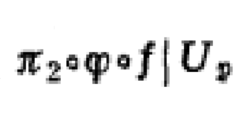
的一个正则值，其中Up为以上所设的某个邻域。

推论 设f∈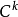 (M，Nⁿ)且Sⁿ为N的 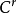子流形，k,r≥1。如果f与S横截，则 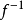（S）或者是空集，或者是余维数为n一s的 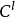子流形，这里l=min(k,r)。

命题2 若M是紧的且S⊂N为闭的，则横截于S的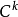 (M，N)中的映射形成一个开子集。2

命题3 若F：AXM→N与S⊂N横截，则Ts是在A中剩余的。

推论1 设f：M→Rⁿ具有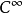 类且S⊂Rⁿ为一子流形。那么使f+v与S横截的向量v∈Rⁿ之集合是剩余的。

推论2 若M是紧流形，则横截于一个闭子流形S⊂Rⁿ的映射集合Ts⊂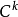 (M,Rⁿ)是开且稠的。

定理4 (Thom)假定M是紧的，S⊂N是闭子流形。与S横截的映射f∈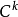 (M，N)之集合是开且稠的2。