定义基本定义

定义1 当一条线段的一个端点被指定为起点．而另一个端点被指定为终点，并且规定由起点到终点的方向叫作这条线段的方向时，那么，这种线段叫作有向线段2．

也可以简单地说，规定了起点和终点的线段叫作有向线段．或者说，规定了方向的线段叫作有向线段．起点为A，终点为B的有向线段用符号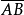 表示．

起点与终点重合的有向线段叫作零有向线段．零有向线段的方向可以任意指定．

定义2 如果两条有向线段方向相同．并且长度相等，就说这两条有向线段相等；规定零有向线段都是相等的2．

必须注意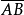， 与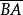 是不相等的．因为它们的方向相反．

配置在轴上的有向线段定义3 当一条直线的正向被指定了以后，那么．这种直线叫作轴(有向直线)2．

若配置在轴上的有向线段的方向和轴的正向相同，那么，这种位置的有向线段叫作轴上的正方向的有向线段；若有向线段的方向和轴的正向相反，那么，这种位置的有向线段叫作轴上的负方向的有向线段．

定义4 轴上的正方向的有向线段的长度，负方向的有向线段的长度的相反数，叫作这条有向线段的数值(代数长)．规定零有向线段的数值为02．

有向线段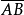 的数值用符号“值 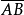”或“AB”表示，而长度(或叫作模)用符号“∣ 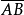∣”表示。

相关定理定理1 设A，B是轴上的任意两点，则AB=﹣BA2

即：AB+BA=0

定理2 (沙尔(Mishel Schasles)定理) 设A，B，C是轴上的任意三点，则以下的关系式总成立，即

AB+BC=AC2

证明 分以下几种情形证明．

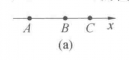
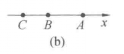
(1)B在A，C之间，并且由A到B的方向和轴的正向相同(图(a))．

由初等几何知道：∣AB∣+∣BC∣=∣AC∣(∣ AB∣表示线段AB的长度)，

而

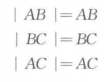
所以有:AB+BC=AC

(2)B在A，C之间，并且由A到B的方向和轴的正向相反(图(b))．由(1)知道：CB+BA=CA，而由定理1知

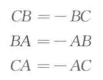
所以有:AB+BC=AC

其余各种情形的证明，可按下图自己完成．

推论(沙尔定理的推广) 设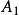,,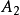,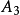......,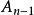,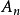(n≥3)是轴上的任意n个点．则关系式2

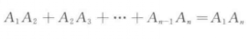
总成立．

有向线段三要素起点、方向和长度，知道了有向线段的起点，它的终点就被方向和长度唯一确定1。

有向线段与向量有向线段不等同于向量。二者的区别是：向量可用有向线段来表示，每一条有向线段对应着一个向量，但每一个向量对应着无数多条有向线段1。