定义

可分多项式在不同的作者的书下有两个略微不同的定义。
最常见的一个定义是：当在一个给定域K上的多项式P(X)在K的代数闭包中有不同的根时，称多项式为可分的。换言之它的互异根的数量需要等于多项式的次数。在多项式因式分解的观点下，这样的多项式是无平方多项式。
第二个定义，当P(X)在K[X]中的每个不可约因子在K的代数闭包中的根互不相同，此时称P(X)是可分的。这意味着每个不可约因子是无平方项的。在这个定义中，可分性依赖于K，比如任何一个不可分的不可约多项式P在它的分裂域上都变成可分的了。并且在这个定义下，每个域上的多项式是可分的，这包含了0特征域和所有有限域。
两个定义对于K上不可约多项式是等价的，这个被用来定义域K的可分扩张。
在条目的余下部分我们只用第一个定义。
一个多项式可分当且仅当它与它的形式导数P'(X)互素1。

详解由于存在所谓的不可分不可约多项式或不可分元素——即这些元素是n次代数的，但它的共轭元素的个数小于n一伽罗瓦群的一般讨论就变得复杂了．对某些特征为p的域，这种复杂化就出现了，这可以用简单的例子加以说明2．

设K=Zp(u)表示模p整数的域Zp的单超越扩张，并设F表示由u^p=t生成的K的子域Zp(u^p)．于是，F是由Zp上的超越元素t的所有有理形式组成．原来的元素u满足F上的一个多项式方程f(x)=x^p—t=o．这个多项式f(x)在F=Zp(t)上实际上是不可约的，这是因为如果f在Zp(t)上可约，根据高斯引理，在t的多项式整环Zp[t]上，f是可约的，但是，由于f(x)=x^p—t对于t来说是线性的，所以这样的因式分解．f(x)=g(x，t)h(x，t)是不可能的．因此f(x)的根u在F上的次数是p．但是f(x)在K上有因式分解:f(x)=x^p一u^p=(x一u)^p.因此它只有一个根u，并且u(虽然它的次数p>1)除了它本身之外没有其他共轭元素．

我们可以用下面的术语来描述上述情况．

定义 域F上的一个n次多项式f(x)，如果它在某个根域N⊇F中有n个不同的根，那么称它在域F上是可分的；否则，称f(X)是不可分的．如果有限扩张K⊇F中每个元素在F上都满足一个可分多项式方程，那么称K在F上是可分的2．

容易检验给定的多项式f(x)=a0+a1x+…+anXⁿ是否是可分的．这也就是，首先根据公式f'(x)=a1+(2×a2)x+…+(n×an)x^(n-1)来定义f(x)的形式导数f'(x)，这里n×an表示an的n次自然倍数．如果这些系数都在实数域中，那么这种导数与微积分学中建立的普通导数是一致的．从形式导数的定义出发，不用任何极限概念，我们可以推导出很多微分法则，例如

(f+g)'=f'+g'，(fg)'=fg'+f'g，(f^m)'=mf^(m-1)f'，等等．

在任意根域N上把f(x)分解成不同线性因子的幂，

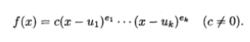
把两边形式地微分，我们看到f'(x)是

与k一1项每项都包含(x-u1)^e1作为因子的和．因此当e1>1时，x—u1可整除f'(x)，而当e1=1时，x一u1就不能整除f'(x)．对e2，…，ek重复上述推理，我们得到f(x)和f'(x)有公因子，除非e1=e2=…=ek=1，即除非f(x)是可分的；因此f(x)在N上是可分的当且仅当f(x)和它的形式导数f'(x)是互素的2．

相关定理f(x)和f'(x)的最大公因式可用F[x]中的欧几里得算法直接计算出来；当F扩张到较大的域上时，它们的最大公因式并不改变．于是我们得到

定理 设f(x)是域F上任意多项式，用欧几里得算法计算f(x)和它的形式导数f'(x)的最大公因式d(x)(首一多项式)．如果d(x)=1，那么，f(x)是可分的；否则f(x)是不可分的．

如果f(x)是不可约的，那么除非f(x)整除g(x)，总有g．c．d．(f(x)，g(x))=1，并且f(x)不能整除任意较低次的非零多项式．因此得到

推论1 任意不可约多项式是可分的，除非它的形式导数是零2．

推论2 特征为∞的域上的任意不可约多项式是可分的2．

这是因为，当n>0，an≠0时，

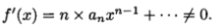
进一步推论是：如果F的特征是∞，那么任意n次不可约多项式f(x)的根域恰恰包含f(x)的n个不同的共轭根．而且，在特征为∞的域上的任意代数数满足一个不可约的因而也是可分的方程，所以特征为∞的域的任意代数扩张，在上述意义之下是可分扩张2．

推论2的结果对于素特征的域是不成立的．例如，在不可约多项式f(x)=x^p—t有形式导数(x^p—t)'=p×x^(p-1)=02．