定义
如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),那么集合A称为集合B的子集,记为A⊆B或 B⊇A,读作“集合A包含于集合B”或集合B包含集合A”。
即:∀a∈A有a∈B,则A⊆B。1
真子集
如果集合A是B的子集,且A≠B,即B中至少有一个元素不属于A,那么A就是B的真子集,可记作:A⊊B**。**
符号语言:若∀a∈A,均有a∈B,且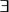 x∈B使x∉A,则A⊊B。
x∈B使x∉A,则A⊊B。
如概述图中,集合A就是集合B的真子集。2
性质一、根据子集的定义,我们知道A⊆A。也就是说,任何一个集合是它本身的子集。
二、对于空集∅,我们规定∅⊆A,即空集是任何集合的子集。
说明:若A=∅,则∅⊆A仍成立。
证明:给定任意集合A,要证明∅是A的子集。这要求给出所有∅的元素是A的元素;但是,∅没有元素。对有经验的数学家们来说,推论“∅没有元素,所以∅的所有元素是A 的元素"是显然的;但对初学者来说,有些麻烦。 因为∅没有任何元素,如何使"这些元素"成为别的集合的元素? 换一种思维将有所帮助。
为了证明∅不是A的子集,必须找到一个元素,属于∅,但不属于A。 因为∅没有元素,所以这是不可能的。因此∅一定是A的子集。
三、若A、B、C是集合,则:
自反性:A=A
反对称性:当且仅当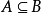 且
且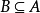 时,
时,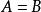
传递性:若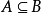 且
且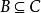 ,则
,则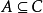
这个命题说明:包含是一种偏序关系。
四、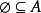 ,
,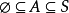
这个命题说明:对任意集合S,S的幂集按包含排序是一个有界格,与上述命题相结合,则它是一个布尔代数。
五、: 对任意两个集合 A 和 B,下列所有表述等价:
A ⊆ B
A ∩ B =A
A ∪ B = B
A−B=A (当A∩B=∅) ;A−B=C?(A∩B)(当A∩B≠∅)
B′ ⊆ A′
这个命题说明:表述 "A ⊆ B " 和其他使用并集,交集和补集的表述是等价的,即包含关系在公理体系中是多余的。
六、假设非空集合A中含有n个元素,则有:
A的子集个数为2n。
A的真子集的个数为2n-1。
A的非空子集的个数为2n-1
A的非空真子集的个数为2n-2。3


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

