定义

测度理论是实变函数论的基础。所谓测度，通俗的讲就是测量几何区域的尺度。 我们知道直线上的闭区间的测度就是通常的线段长度； 平面上一个闭圆盘的测度就是它的面积。

形成意义定理的形成纵观勒贝格积分和勒贝格－斯蒂尔杰斯积分理论，不难发现它们都有三个基本要素。

第一，一个基本空间（即n维欧几里得空间R）以及这个空间的某些子集构成的集类即L（勒贝格）可测集或某L－S（勒贝格-斯蒂尔杰斯）可测集全体，这个集类对集的代数运算和极限运算封闭。

第二，一个与这个集类有关的函数类（即L可测函数或某L-S可测函数全体）。

第三，一个与上述集类有关的测度（即L测度或某L-S测度）。

在三个要素的基础上，它们都是运用完全类似的定义和推理过程获得完全类似的一整套测度、可测函数、积分的定理（见勒贝格积分、贝尔函数）。测度论正是基于这些基本共同点所形成一般理论。

意义对于更一般的集合，我们能不能定义测度呢？ 比如直线上所有有理数构成的集合，它的测度怎么衡量呢？

一个简单的办法， 就是先在每个有理点上找一个开区间覆盖它，就好比给它带个“帽子”。因为有理数集是可列集（就是可以像排自然一样排好队，一个个数出来，也叫可数集，见集合论），所以我们可以让第n个有理数上盖的开区间长度是第一个有理数（比方是1）上盖的开区间长度的2^n分之一。 这样所有那些开区间的长度之和是个有限值（就是1上的开区间长度的2倍）。

我们让1上的开区间逐渐缩小趋向于一个点，那么所有区间的总长度也相应缩小，趋向于长度0。 这样我们就说有理数集的测度是0。 用上面这种方法定义的测度也叫外测度。

一个几何区域有了测度，我们就可以定义上面的函数的积分，这是推广的黎曼积分。

比如实数上的狄利克雷函数D(x)=1(如果x是有理数)，0（如果x是无理数）。 如果按照通常的理解，我们发现狄利克雷函数在整个数轴上的定积分不存在；但是按照上面讲的有理数的测度，我们就可以求出它的定积分是0。

实直线上的测度如下给出：

设E是实数集，考虑可数个区间(aj,bj)满足对任何x∈E,都有某个j,使得x∈(aj,bj);考虑所有情形下和(b1-a1)+(b2-a2)+..的下确界称为E的外测度

如果对任何集合F都有E∩F和F\E的外测度之和等于F的外测度，称E可测，定义其测度等于外测度

直观含义上面已经解释过了

数学定义测度的相关数学定义：

集函数：设Ψ是上的非空集合类。若对于每一个A∈Ψ,都有一个实数或者±∞之一与之对应(为确定起见，下面假定只取+∞)，记为φ(A)，且至少有一个A∈Ψ,使得φ(A)取有限值，称φ(A)为定义在Ψ上的集函数。

(1)若对任意的正整数n以及任意的Ai∈Ψ，i=1，2……，n，Ai∩Aj=O;(i≠j)，且(A1∪A2∪…Ai∪…An)∈Ψ，有：

φ(A1∪A2∪…Ai∪…An)=∑[φ(A1)∪φ(A2)∪…φ(Ai)∪…φ(An)]，1

则称φ在Ψ上具有有限可加性，也称φ是Ψ上的有限可加集函数。

(2)若对可列集的Ai∈Ψ，i=1，2……，n，Ai∩Aj=O;(i≠j)，且(A1∪A2∪…Ai∪…A∞)∈Ψ，有

φ(A1∪A2∪…Ai∪…A∞)=∑[φ(A1)∪φ(A2)∪…φ(Ai)∪…φ(A∞)]，

则称φ在Ψ上具有完全可加性或者б-可加性，也称φ是Ψ上的б-可加集函数或者广义测度。

(3)若对每一个A∈Ψ，φ(A)都取有限值，则称φ为上的有限集函数。如果对每一个A∈Ψ，存在一个集合序列⊂Ψ，使得

A⊂(A1∪A2∪…Ai∪…A∞)，φ(An)с}∈φ，那么称ƒ为E上关于(Χ,φ)的可测函数，也称为E上的φ)可测函数。这种可测函数是L可测函数、L-S可测函数等概念的直接推广。它有许多等价定义方式,并且具有L可测涵数所具有的代数性质及极限性质。定义在E上的复值函数ƒ，如果它的实部、虚部都是可测函数，那么就称ƒ为E上的可测函数。可测空间、可测集、以及可测函数等概念原则上并不涉及测度。

测度空间设Χ是非空集,E是Χ上的集类,定义在E上的函数称为集函数（因为自变元是属于E，它是Χ的子集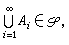）。设R是Χ上的环，μ是定义在R上的取非负的广义实值(可以取值+∞)的集函数，如果满足：①μ(═)=0(═是空集)；②(可列可加性)对任何一列互不相交的 An∈R(n=1,2…,),并且：式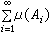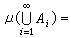①，有：式②=③，则称μ为环R上的测度。设(Χ,φ)是一个可测空间,μ是定义在φ上的测度，则称(Χ,φ),μ)是测度空间。特别，(R1,L,m)及(R1,Lg,mg)分别称为（直线上的）L测度空间和L-S 测度空间。测度空间(Χ,φ,μ)中的测度μ 除了平移、反射不变性以及余集(因为 X可能不在S中）的性质外,具有勒贝格测度m的其他性质。由于φ是σ环,对集的极限运算封闭，所以测度空间是建立具有良好的极限性质的积分的基础。

设A是可测空间(Χ，φ)中可测集。如果有一列可测集{An},μ(An)