定义

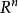在线性代数中，正交变换是线性变换的一种。对一个由空间投射到同一空间的线性转换，如果转换后的向量长度与转换前的长度相同，则为正交变换。1

其中在空间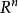内，n表示维度。

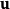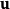对于正交变换T以及两个向量和，和之内积等于正交转换后之向量和之内积。

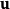
其中N为向量长度，u[n]和v[n]分别为和之元素，正交变换不会影响转换前后向量间的夹角和内积长度。

在矩阵表示形式上，如果为正交变换，则为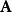正交矩阵，对于正交变换之正交矩阵，其每个列互为正交，令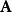为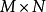之矩阵，取两个不相同的列和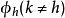遵守下列关系。

等价刻画设σ是n维欧式空间V的一个线性变换，于是下面4个命题等价

1.σ是正交变换；

2.σ保持向量长度不变，即对于任意α∈V，丨σ(α)丨=丨α丨；

3.如果ε_1,ε_2,...,ε_n是标准正交基，那么σ(ε_1),σ(ε_2),...,σ(ε_n)也是标准正交基；

4.σ在任意一组标准正交基下的矩阵是正交矩阵。

正交矩阵定义：n级实矩阵A称为正交矩阵，如果A*A=E。(A*表示A的共轭转置，E是单位矩阵)

分类设A是n维欧式空间V的一个正交变换σ在一组标准正交基下的矩阵1

若丨A丨=1，则称σ为第一类正交变换，

若丨A丨=-1，则称σ为第二类正交变换。

2

性质（1）正交变换不会改变向量间的正交性，如果和正交，则和亦为正交。

（2）如果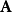和皆为正交矩阵，则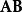亦为正交矩阵。

（3）如果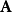为正交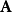矩阵，的反矩阵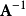亦为正交矩阵。

（4）正交变换容易做反运算。

（5）对于正交变换，如果和可以做内积，和做内积之值等于和做内积之值。

应用正交变换的种类非常的广，像是discrete Fourier transform、discrete cosine, sine, Hartley transforms、Walsh Transform, Haar Transform等都属于正交变换。对矩阵做旋转或是镜射也属于正交变换。