定义

三等分角线（Trisectrix）是可以用来三等分任意角的曲线。

性质三角形有关角三等分线的交点构成的三角形有许多美妙的性质。

定理一：与任意△ABC每边相邻的每两个优角相邻的三等分线的反向延长线的交点构成正三角形，且其边长为 。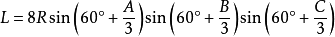

定理二：三角形任意一个优角与另两个劣角中，与每边相邻的每两个角相邻的三等分线（或其反向延长线）的交点构成正三角形，且边BC、AC、AB所正对的正三角形的边长分别是：

;

;

.

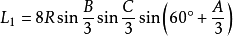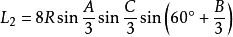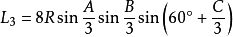定理三：任意△ABC任意一边相邻的两个优角相邻三等分线的反向延长线的交点，及与这边相邻的劣角与外角相邻的三等分线（或其反向延长线）的交点构成正三角形，且边BC、AB、AC所正对的三角形的边长分别是：

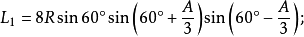
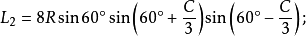
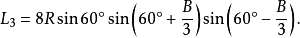
定理四：任意△ABC任意一边相邻的两个外角相邻三等分线的交点，及与这边相邻的劣角与优角相邻三等分线（或其反向延长线）的交点构成正三角形，且点A、B、C所对的正三角形的边长分别是：

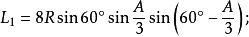
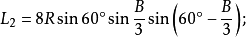
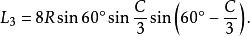
定理五：任意△ABC没有公共顶点的任意一个劣角、一个优角及其夹边所对的另两个外角中，与每边相邻的每两个角相邻的三等分线（或其反向延长线）的交点构成正三角形，且六个正三角形的边长分别是：

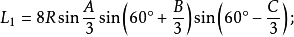
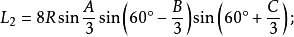
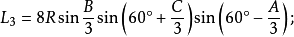
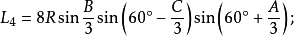
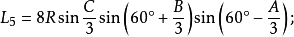
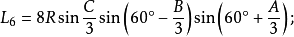
定理六：任意△ABC任意两个优角及其夹边所对的两个外角中，与每边相邻的每两个角相邻的三等分线（或其反向延长线）的交点构成正三角形，且边BC、AB、AC所对的正三角形的边长分别是：

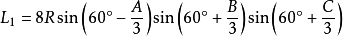
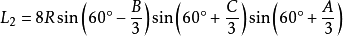
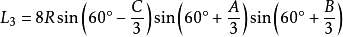
**定理七：**任意一边相邻的两个劣角的相邻三等分线的交点，及与这边相邻的优角与外角的相邻三等分线的交点构成正三角形，且点A、B、C所对的正三角形的边长分别是：

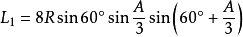
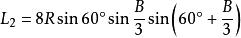
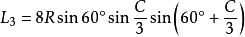1

类型

蜗牛三等分角线（有些文献直接称此曲线为三等分角线）
马克劳林三等分角线
等边三叶（Equilateraltrefoil）
契尔恩豪森三次曲线
丢勒的大青叶（Durer'sfolium）
三次抛物线（Cubicparabola）
偏心率为2的双曲线
三叶的玫瑰线
抛物线

相关曲线与三等分角线相关的曲线是等分角线（sectrix），是可以将任意角分为整数个的曲线。以下是一些等分角线：
阿基米德螺线
割圆曲线
马克劳林等分角线
Ceva等分角线（SectrixofCeva）
Delanges等分角线（SectrixofDelanges）