简介

线性方程组是各个方程关于未知量均为一次的方程组(例如2元1次方程组）。对线性方程组的研究，中国比欧洲至少早1500年，记载在公元初《九章算术》方程章中。

线性方程组有广泛应用，熟知的线性规划问题即讨论对解有一定约束条件的线性方程组问题。

定义xj表未知量，aij称系数，bi称常数项。

称为系数矩阵和增广矩阵。若x1=c1，x2=c2，…，xn=cn代入所给方程各式均成立，则称（c1，c2，…，cn）为一个解。若c1，c2，…，cn不全为0，则称（c1，c2，…，cn）为非零解。若常数项均为0，则称为齐次线性方程组，它总有零解（0，0，…，0）。两个方程组，若它们的未知量个数相同且解集相等，则称为同解方程组。线性方程组主要讨论的问题是：

①一个方程组何时有解。

②有解方程组解的个数。

③对有解方程组求解，并决定解的结构。这几个问题均得到完满解决：所给方程组有解，则秩(A）=秩（增广矩阵）；若秩(A）=秩=r，则r=n时，有唯一解；r0的情形下，A有一个r阶子式D不等于零，设

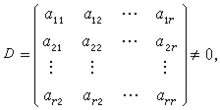
于是方程组⑴与仅含有前r个方程的方程组同解。可将前r个方程改写为

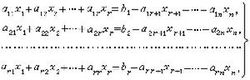
方程组⑵的一般解公式为 x1=D1/D,x2=D2/D，…，xr=Dr/D， ⑶

式中Dj(j=1,2，…，r）是把D的第j列换成方程组⑵的右端的列所得到的一个r阶行列式，即

因而x1,x2，…，xr可由其余的未知量xr+1,xr+2，…，xn线性表出，xr+1，xr+2，…，xn称为自由未知量。

当r