一般地，用纯粹的大于号“>”、小于号“0。1

二元一次不等式是指含有两个未知数(即二元)，并且未知数的次数是1次(即一次)的不等式。

有序实数对可以看成直角坐标平面内点的坐标。于是二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合。

一般地， 在直角坐标系中，二元一次不等式表示某侧所有点组成的平面区域。我们把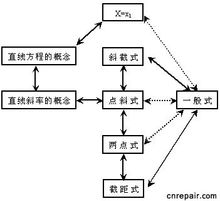直线画成虚线时，表示区域不包括边界。而不等式表示区域包括边界时，则把边界画成实线：不等式组表示的平面区域是各个不等式所表示的平面点集的交集，因而是各个不等式所表示的平面区域的公共部分。

在教学中发现，由直线方程一般式的系数特征，可判断直线位置关系的方法，类比可得到由二元一次不等式Ax+By+C > 0的系数特征(A，B的符号特征)，确定二元一次不等式ax+By+c > 0表示的平面区域的规律，下面给予介绍，以供参考。

（1）若A>0，B>0，则二元一次不等式ax+By+C > 0表示直线Az+By+C=0右上方的平面区域；

（2） A>0，B0表示直线Ax十By十C=0右下方的平面区域；

（3）A0时，二元一次不等式Ax+By+C > 0表示直线Ax十By+C=0左上方的平面区域；

（4） A0时，二元一次不等式Ax+ By+C> 0表示直线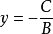 上方的平面区域；

（6）A=0，B 0表示直线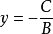下方的平面区域；

（7）A>0，B=0时，二元一次不等式Ax+ By+C> 0表示直线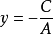右侧的平面区域；

（8）A0表示直线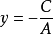左侧的平面区域。2

一般地，关于两个未知数的几个二元一次不等式合在一起，就组成一个二元一次不等式组。

用加减法解不等式的时候，不用去记住很多代入法要注意的小技巧，特别是考试时比较紧张，如果要记住太多很容易出错的。这种相加法，用熟之后过程可以不用这么繁复，可以少写一两步。

特别注意，根据不等式性质，不等号方向相同的两式子，只能相加，不能相减。

不等号方向相反时，两边才能相减，相减后的不等号方向与被减式相同。实际这跟两式相加一样的，只要把式子两边交换，">号"会变"