被加数是求和法中的一项,类似于减法中的被减数,在加法中,被加数和加数的性质是一样的,只不过为了和减法的被减数搭配起来一起学习而提出来的概念。
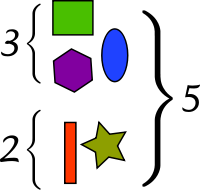
加法是基本的四则运算之一,它是指将两个或者两个以上的数、量合起来,变成一个数、量的计算。表达加法的符号为加号“+”。进行加法时以加号将各项连接起来。加法(通常用加号“+”表示)是算术的四个基本操作之一,其余的是减法,乘法和除法。 例如,在下面的图片中,共有三个苹果和两个苹果的组合,共计五个苹果。 该观察结果等同于数学表达式“3 + 2 = 5”,即“3加2等于5”,3就可以看成被加数,2看成加数,5就是和。1

加法已经被用于建立了无数的物理过程。 即使添加自然数的简单情况,也有许多可能的解释和更多的视觉表现。
组合可能最基本的加法解释在于组合:
当两个或多个不相交的集合被组合成单个集合时,单个集合中的对象数量是原始集合中对象数量的总和。
这种解释很容易可视化。 它也适用于高等数学;对于它激发的严格定义,请参见下面的自然数字。
一个可能的解决方案是考虑可以容易地分割的对象的集合,例如馅饼。杆不仅可以组成棒的集合,还可以将杆连接在一起,这又说明了加法的另一个概念:不添加棒,而是添加杆的长度。
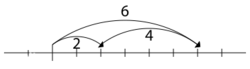
对加法的第二个解释来自于将初始长度延长给定长度:
当原始长度延长给定量时,最终长度是原始长度和延伸长度之和,那么在这里原始长度就可以看成被加数,延伸长度就是加数,最终长度就是和。
一般来说,在一个集合F上定义一个二元关系“+”,满足:
Ⅰ交换律:对任意的a,b∈F,a+b=b+a∈F;
Ⅱ结合律:对任意的a,b,c∈F,a+ (b+c) = (a+b) +c;
Ⅲ单位元:存在一个元素 0 ∈F,满足对任意的 a ∈F,a+ 0 = 0 +a=a;
Ⅳ 逆元:对任意的a∈F,存在一个元素 -a∈F,满足a+ (-a) = 0。
“+”称作定义在集合F上的加法。
“+”是加号,加号前面和后面的数是加数,“=”是等于号,等于号后面的数是和。
100(加数) +(加号) 300(加数) =(等于号) 400(和)2
加法本质是完全一致的事物也就是同类事物的重复或累计,是数字运算的开始,不同类比如一个苹果+一个橘子其结果只能等于二个水果就存在分类与归类的关系。减法是加法的逆运算;乘法是加法的特殊形式;除法是乘法的逆运算;乘方是乘法的简便形式;开方是乘方的逆运算;对数是在乘方的各项中寻找规律;由对数而发展出导数;然后是微分和积分。数字运算的发展,是更特殊的情况,更高度重复下的规律。3


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

