基本原理
两个数的最大公约数是指能同时整除它们的最大正整数。1
设两数为a、b(a≥b),求a和b最大公约数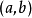 的步骤如下:
的步骤如下:
(1)用a除以b(a≥b),得 。
。
(2)若 ,则
,则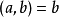 ;
;
(3)若 ,则再用b除以
,则再用b除以 ,得
,得 .
.
(4)若 ,则
,则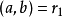 ;若
;若 ,则继续用
,则继续用 除以
除以 ,......,如此下去,直到能整除为止。
,......,如此下去,直到能整除为止。
其最后一个余数为0的除数即为 的最大公约数。
的最大公约数。
证明设两数为a、b(a>b),用 表示a,b的最大公约数,r=a (mod b) 为a除以b的余数,k为a除以b的商,即
表示a,b的最大公约数,r=a (mod b) 为a除以b的余数,k为a除以b的商,即 。辗转相除法即是要证明
。辗转相除法即是要证明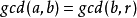 。
。
第一步:令 ,则设
,则设
第二步:根据前提可知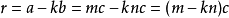
第三步:根据第二步结果可知, 也是
也是 的因数
的因数
第四步:可以断定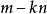 与
与 互质(这里用反证法进行证明:设
互质(这里用反证法进行证明:设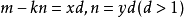 ,则
,则 ,则
,则 ,则a与b的一个公约数
,则a与b的一个公约数 ,故c非a与b的最大公约数,与前面结论矛盾,因此c也是b与r的最大公约数)从而可知
,故c非a与b的最大公约数,与前面结论矛盾,因此c也是b与r的最大公约数)从而可知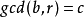 ,继而
,继而 。
。
证毕
注:以上步骤的操作是建立在刚开始时 的基础之上的,即m与n亦互质。1
的基础之上的,即m与n亦互质。1
算法描述用辗转相除法确定两个正整数 a 和 b(a≥b) 的最大公因数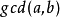 :
:
当 时,
时, ;否则
;否则 递归或循环运算得出结果。
递归或循环运算得出结果。
算法流程图如下:

伪代码描述如下:
function gcd(a,b) {if b0 return gcd(b,a mod b);else return a;}示例例1123456 和 7890 的最大公因数是 6,这可由下列步骤(其中,“a mod b”是指取 a ÷ b 的余数)看出:
|| ||
例2已知不定方程为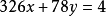 ,利用辗转相除法求出一组整数解
,利用辗转相除法求出一组整数解
解:求 的算式为:
的算式为:









所以
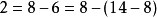
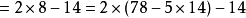

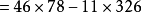 即
即

所以

所以 是不定方程
是不定方程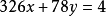 的一组解。
的一组解。
代码实现c语言int GCD(int a,int b){ return b==0?a:GCD(b,a%b);}C++语言实现#includeusing namespace std;int a , b , a1 , b2 , l;int gcd(int x , int y){ if(!y) return x;else return gcd(y , x%y); }int main(){cout b;if(a > b)ans = gcd(a , b);else ans = gcd(b , a);cout


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

