简介
在数学中,抛物线是一个平面曲线,它是镜像对称的,并且当定向大致为U形(如果不同的方向,它仍然是抛物线)。它适用于几个表面上不同的数学描述中的任何一个,这些描述都可以被证明是完全相同的曲线。
抛物线的一个描述涉及一个点(焦点)和一条线(该线)。焦点并不在于准则。抛物线是该平面中与阵线和焦点等距的点的轨迹。抛物线的另一个描述是作为圆锥截面,由右圆锥形表面和平行于与锥形表面相切的另一平面的平面的交点形成。第三个描述是代数。抛物线是例如二次函数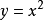 的图。
的图。
垂直于准线并通过焦点的线(即通过中间分解抛物线的线)被称为“对称轴”。与对称轴相交的抛物线上的点被称为“顶点”,并且是抛物线最锋利弯曲的点。沿着对称轴测量的顶点和焦点之间的距离是“焦距”。 “直肠直肠”是抛物线的平行线,并通过焦点。抛物线可以向上,向下,向左,向右或向另一个任意方向打开。任何抛物线都可以重新定位并重新定位,以适应任何其他抛物线 - 也就是说,所有抛物线都是几何相似的。
抛物线具有这样的性质,如果它们由反射光的材料制成,则平行于抛物线的对称轴行进并撞击其凹面的光被反射到其焦点,而不管抛物线在哪里发生反射。相反,从焦点处的点源产生的光被反射成平行(“准直”)光束,使抛物线平行于对称轴。声音和其他形式的能量也会产生相同的效果。这种反射性质是抛物线的许多实际应用的基础。
抛物线具有许多重要的应用,从抛物面天线或抛物线麦克风到汽车前照灯反射器到设计弹道导弹。它们经常用于物理,工程和许多其他领域。
发展历程Apollonius 所著的八册《圆锥曲线》(Conics)集其大成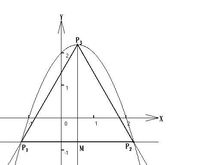 ,可以说是古希腊解析几何学一个登峰造极的精擘之作。今日大家熟知的 ellipse(椭圆)、parabola(抛物线)、hyperbola(双曲线)这些名词,都是 Apollonius 所发明的。当时对于这种既简朴又完美的曲线的研究,乃是纯粹从几何学的观点,研讨和圆密切相关的这种曲线;它们的几何乃是圆的几何的自然推广,在当年这是一种纯理念的探索,并不寄望也无从预期它们会真的在大自然的基本结构中扮演着重要的角色。
,可以说是古希腊解析几何学一个登峰造极的精擘之作。今日大家熟知的 ellipse(椭圆)、parabola(抛物线)、hyperbola(双曲线)这些名词,都是 Apollonius 所发明的。当时对于这种既简朴又完美的曲线的研究,乃是纯粹从几何学的观点,研讨和圆密切相关的这种曲线;它们的几何乃是圆的几何的自然推广,在当年这是一种纯理念的探索,并不寄望也无从预期它们会真的在大自然的基本结构中扮演着重要的角色。
标准方程标准方程右开口抛物线: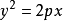
左开口抛物线: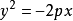
上开口抛物线: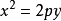
下开口抛物线: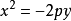
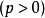 [p为焦准距]
[p为焦准距]
特点在抛物线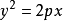 中,焦点是
中,焦点是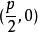 ,准线的方程是
,准线的方程是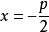 ,离心率
,离心率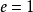 ,范围:
,范围: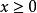 ;
;
在抛物线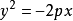 中,焦点是
中,焦点是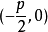 ,准线的方程是
,准线的方程是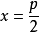 ,离心率
,离心率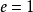 ,范围:
,范围: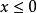 ;
;
在抛物线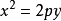 中,焦点是
中,焦点是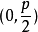 ,准线的方程是
,准线的方程是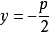 ,离心率
,离心率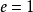 ,范围:
,范围: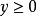 ;
;
在抛物线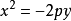 中,焦点是
中,焦点是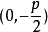 ,准线的方程是
,准线的方程是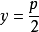 ,离心率
,离心率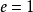 ,范围:
,范围: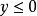 ;
;
四种方程抛物线四种方程的异同
共同点:
①原点在抛物线上,离心率e均为1 ②对称轴为坐标轴;
③准线与对称轴垂直,垂足与焦点分别对称于原点,它们与原点的距离都等于一次项系数的绝对值的1/4
不同点:
①对称轴为x轴时,方程右端为±2px,方程的左端为y^2;对称轴为y轴时,方程的右端为±2py,方程的左端为x^2;
②开口方向与x轴(或y轴)的正半轴相同时,焦点在x轴(y轴)的正半轴上,方程的右端取正号;开口方向与x(或y轴)的负半轴相同时,焦点在x轴(或y轴)的负半轴上,方程的右端取负号。
切线方程抛物线y2=2px上一点(x0,y0)处的切线方程为: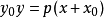
抛物线y2=2px上过焦点斜率为k的方程为:y=k(x-p/2)
相关参数**(对于向右开口的抛物线y2=2px)**
离心率:e=1(恒为定值,为抛物线上一点与准线的距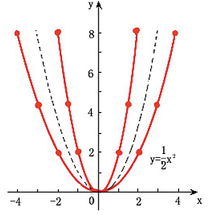 离以及该点与焦点的距离比)
离以及该点与焦点的距离比)
焦点:(p/2,0)
准线方程l:x=-p/2
顶点:(0,0)
通径:2P ;定义:圆锥曲线(除圆外)中,过焦点并垂直于轴的弦
定义域:对于抛物线y2=2px,p>0时,定义域为x≥0,p0时,值域为y≥0,p0),焦点F坐标为(0,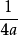 )
)
根据抛物线的定义知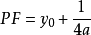
又抛物线导数为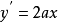
所以切线PN的斜率为2ax0,方程为y-y0=2ax0(x-x0)
求点T的坐标,令x=0,联立抛物线方程得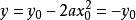
则点T坐标为(0,-y0)所以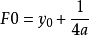
所以PF=FT,∠FTP=∠FPT,
又∠FPT=∠MPN
所以∠FTP=∠MPN
MP平行于y轴1
扩展公式抛物线:y = ax2 + bx + c (a≠0)
就是y等于ax 的平方加上 bx再加上 c
a > 0时开口向上
a
c = 0时抛物线经过原点
b = 0时抛物线对称轴为y轴
还有顶点式y = a(x-h)2 + k
h是顶点坐标的x
k是顶点坐标的y
一般用于求最大值与最小值
抛物线标准方程:y2=2px
它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0) 准线方程为x=-p/2
由于抛物线的焦点可在任意半轴,故共有标准方程y2=2px,y2=-2px,x2=2py,x2=-2py
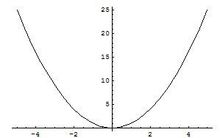
二次函数图象在平面直角坐标系中作出二次函数y=ax2+bx+c的图像,可以看出,在没有特定定义域的二次函数图像是一条永无止境的抛物线。 如果所画图形准确无误,那么二次函数图像将是由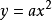 平移得到的。
平移得到的。
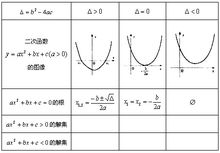 二次函数图像是轴对称图形。对称轴为直线
二次函数图像是轴对称图形。对称轴为直线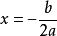
对称轴与二次函数图像唯一的交点为二次函数图象的顶点P。
特别地,当b=0时,二次函数图像的对称轴是y轴(即直线x=0)。是顶点的横坐标(即x=?)。
a,b同号,对称轴在y轴左侧
a,b异号,对称轴在y轴右侧
二次函数图像有一个顶点P,坐标为P(h,k)。
当h=0时,P在y轴上;当k=0时,P在x轴上。即可表示为顶点式y=a(x-h)2+k(a≠0)
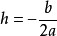 ,
,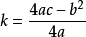 。
。
二次项系数a决定二次函数图像的开口方向和大小。
当a>0时,二次函数图象向上开口;当a0,与b同号时(即ab>0),对称轴在y轴左**; 因为对称轴在左边则对称轴小于0,也就是- b/2a0,与b异号时(即ab**0, 所以b/2a要小于0,所以a、b要异号。****
可简单记忆为左同右异,即当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab0有两个实数根;
⑵△=b2-4ac=0有两个一样的实数根;
⑶△=b2-4ac


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

