全错位排列被著名数学家欧拉(Leonhard Euler,1707-1783)称为“组合数论的一个妙题”的“装错信封问题”的两个特例。
简介基本简介“装错信封问题”是由当时最有名的数学家约翰·伯努利(Johann Bernoulli,1667-1748)的儿子丹尼尔·伯努利(DanidBernoulli,1700-1782)提出来的,大意如下:
一个人写了n封不同的信及相应的n个不同的信封,他把这n封信都装错了信封,问都装错信封的装法有多少种?
公式证明n个相异的元素排成一排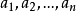 。则
。则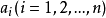 不在第i位的排列数为:
不在第i位的排列数为:
证明:
设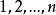 的全排列
的全排列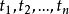 的集合为I,而使
的集合为I,而使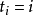 的全排列的集合记为
的全排列的集合记为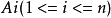 ,
,
则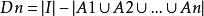 .
.
所以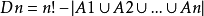 .
.
注意到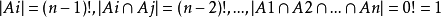 。
。
由容斥原理:
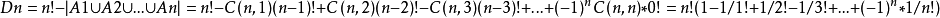
研究错排问题的方法枚举法对于情况较少的排列,可以使用枚举法。
当n=1时,全排列只有一种,不是错排,D1= 0。
当n=2时,全排列有两种,即1、2和2、1,后者是错排,D2= 1。
当n=3时,全排列有六种,即1、2、3;1、3、2;2、1、3;2、3、1;3、1、2;3、2、1,其中只有有3、1、2和2、3、1是错排,D3=2。用同样的方法可以知道D4=9。
最小的几个错排数是:D1= 0,D2= 1,D3=2,D4= 9,D5= 44,D6= 265,D7= 1854.1
递推数列法对于排列数较多的情况,难以采用枚举法。这时可以用递归思想推导错排数的递回关系式。
显然 ,
,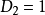 。当
。当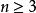 时,不妨设n排在了第k位,其中k≠n,也就是
时,不妨设n排在了第k位,其中k≠n,也就是 。那么考虑第n位的情况。
。那么考虑第n位的情况。
当k排在第n位时,除了n和k以外还有n-2个数,其错排数为Dn-2。
当k不排在第n位时,那么将第n位重新考虑成一个新的“第k位”,这时的包括k在内的剩下n-1个数的每一种错排,都等价于只有n-1个数时的错排(只是其中的第k位会换成第n位)。其错排数为Dn-1。
所以当n排在第k位时共有Dn-2+Dn-1种错排方法,又k有从1到n-1共n-1种取法,我们可以得到:

在上面我们得到 从这个公式中我们可以推出Dn的通项公式,方法如下:
从这个公式中我们可以推出Dn的通项公式,方法如下:
为书写方便,记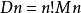 ,则
,则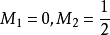
当n大于等于3时,由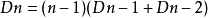 ,即
,即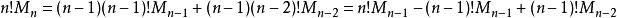 。 所以,
。 所以, 。
。
于是有
将上面式子分边累加,得
因此,我们得到错排公式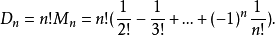
多项式模拟 错排,
错排,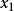 需排在
需排在 、
、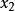 需排在
需排在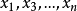 如此类推。
如此类推。
记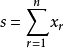 ,错排结果为
,错排结果为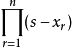 中
中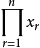 的系数
的系数
记 为基本对称多项式,
为基本对称多项式,
从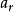 选出
选出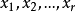 ,然后从
,然后从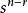 选出
选出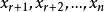 ,组成
,组成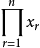
从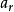 选出r个x有
选出r个x有 种可能,从
种可能,从 选出其余的n-r个x有
选出其余的n-r个x有 种可能3
种可能3
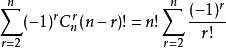
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

