定义
设
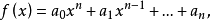
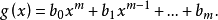 定义下列
定义下列 阶行列式
阶行列式
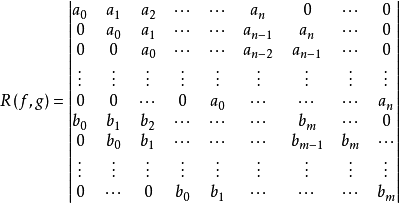 为
为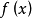 与
与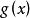 的结式或称
的结式或称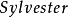 行列式。1
行列式。1
相关定理显然,根据定义我们可以有下列判断两个多项式存在公根的定理,具体证明过程可参考后文参考文献。
定理1多项式 与
与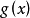 有公根(在复数域中)的充分必要条件是它们的结式
有公根(在复数域中)的充分必要条件是它们的结式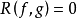 。1
。1
推论1多项式 与
与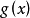 互素的充分必要条件是它们的结式
互素的充分必要条件是它们的结式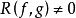 。
。
定理2设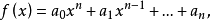
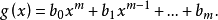
 的根为
的根为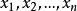 ,
,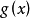 的根为
的根为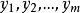 ,则
,则 与
与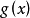 的结式为
的结式为
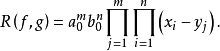
定义2利用结式,可定义多项式的判别式如下。
多项式
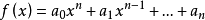 的判别式定义为
的判别式定义为
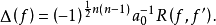
定理3多项式
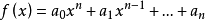 的判别式等于
的判别式等于
 其中
其中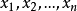 为
为 的根。
的根。
推论2多项式 有重根的充分必要条件是它的判别式
有重根的充分必要条件是它的判别式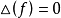 。1
。1


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

