线性流形(linear manifold)是几何学中的常用概念,即Pn中的直线,二维平面,三维平面,…,n-1维平面的统称。设A是线性空间R中的真子集,若对x,x'∈A,θ,θ'∈K,θ+θ'=1,必有θx+θ'x'∈A,就称A是线性流形。设M是R中的线性子空间,x0是R中一点,则集M+x0是一线性流形;反之,每一线性流形可表成M+x0的形式。 线性流形表示式A=M+x0中的子空间M,称做A的平行子空间。若两个线性流形A和B具有相同的平行子空间,就说A和B相互平行。以经0点的直线L0作为平行子空间的线性流形L叫做直线, 以经0点的超平面P0作为平行子空间的线性流形P叫做超平面。两个相互平行的线性流形必或是重合,或是不相交。线性空间中的线性流形是平行子空间的一个平移,而超平面是全空间中的最大线性流形。当人们想把整个空间划分成各个区域时,应用超平面的概念,将使其几何形象特别鲜明1。
基本介绍所谓线性空间V的线性流形,即为
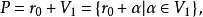 其中
其中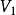 是
是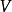 的子空间,
的子空间,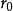 是V的固定向量,且
是V的固定向量,且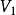 的维数称为线性流形P的维数,一维线性流形称为直线,二维线性流形称为平面,更高维的线性流形称为超平面2。
的维数称为线性流形P的维数,一维线性流形称为直线,二维线性流形称为平面,更高维的线性流形称为超平面2。
相关性质定理1 设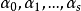 是
是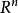 的任意
的任意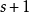 个向量,且
个向量,且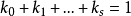 ,则形如
,则形如
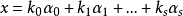 的所有向量组成一个维数等于向量组
的所有向量组成一个维数等于向量组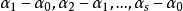 的秩的线性流形P。
的秩的线性流形P。
定理2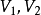 是V的子空间,而
是V的子空间,而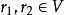 ,则
,则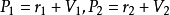 相等的充要条件是
相等的充要条件是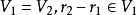 。
。
由线性流形定义的关系式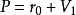 或
或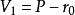 可看出,线性流形P是从线性子空间平行移动一个向量
可看出,线性流形P是从线性子空间平行移动一个向量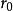 所得,而定理2则说明,用平行移动得到所给流形P的那个线性空间
所得,而定理2则说明,用平行移动得到所给流形P的那个线性空间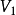 是唯一确定的。
是唯一确定的。
定理3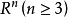 中任意两条直线包含在某个三维线性流形中。
中任意两条直线包含在某个三维线性流形中。
定理4 空间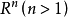 的两条直线
的两条直线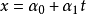 和
和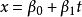 位于一个平面内的充要条件是
位于一个平面内的充要条件是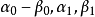 线性相关。
线性相关。
推论1 两条直线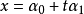 和
和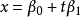 穿过一点但不重合的充要条件是
穿过一点但不重合的充要条件是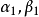 线性无关,而
线性无关,而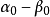 可用
可用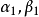 线性表出。
线性表出。
定理5 空间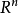 的两个维数分别为k和h的线性流形P和Q包含在一个维数
的两个维数分别为k和h的线性流形P和Q包含在一个维数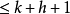 的线性流形中。
的线性流形中。
定理6 如果空间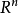 的两个维数分别为k和h的线性流形P和Q有一个公共向量
的两个维数分别为k和h的线性流形P和Q有一个公共向量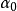 ,则
,则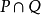 是一个维数
是一个维数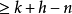 的线性流形2。
的线性流形2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

