向量线(vector line)是向量场中具有特定意义的曲线，指其切线方向与场中向量一致的向量场中的曲线。设f是定义在区域Ω⊆R3上的向量场，Γ是Ω中的光滑曲线，若Γ上每一点处的切向量的方向与f在该点的方向一致，则Γ称为场f的向量线。例如势场f的向量线是它的势函数的梯度线，即这个势函数变化最快的线。若f是稳定流动(即与时间无关)的流体的速度场，则它的向量线是流体质点的移动轨迹，称为流线，若f是引力场，则相应的向量线称为力线1。

基本介绍我们知道，在稳定流动的流体中，质点的瞬时运动方向是该点的速度方向，这就是说，流体中质点的运动轨迹的切线方向，就是速度方向，这条轨迹称为流****线。这就是一般向量场中的向量线概念。

设

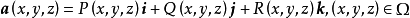为向量场， 为 中的一条曲线。若 上的每一点处的切线方向都与场向量在该点的方向一致，则称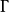 为向量场 的向量线。静电场中的电力线、磁场中的磁力线等都是向量线的实际例子2。

向量线的方程设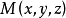为向量线上任一点，则其矢量方程为

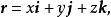那么

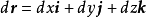就是向量线在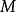点处的切向量。由定义，它与在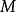点处的场向量共线，因此

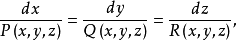这就是向量线所满足的方程，如果解出它的话，一般就得到向量线族。如果再利用过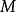点这个条件，就得到过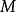点的向量线。一般来说，向量场中每一点有一条且仅有一条向量线通过它，向量线族充满了向量场所在的空间。

例1由电磁学中的Coulomb定律，在位于原点的点电荷q(这里q表示电荷大小)所产生的静电场中，任何一点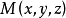处的电场强度为

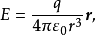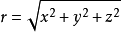其中为点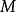到原点的距离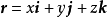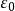，，为真空介电常数。

将E具体写出来就是

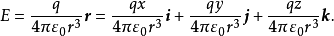由于

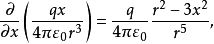
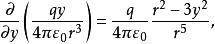
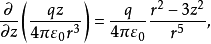所以

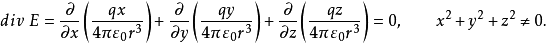
1.设S是以原点为心，R为半径的球面，定向取外侧。注意到在球面S上恒有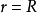，且E的方向与球面S的外法向量的方向相同，因此从内部穿出球面S的通量(称为电通量)为

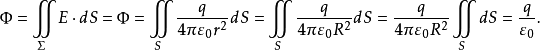
2. 设为任意一张光滑或分片光滑的封闭曲面。

(i) 如果内不含原点。记所包围的区域为，则由Gauss公式得

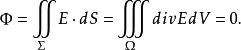
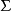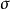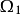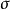(ii) 如果内含有原点，那么不能直接用Gauss公式。在曲面所包围的区域内取一个以原点为心的小球面，定向取内侧。记为介于与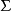之间的区域。由Gauss 公式得

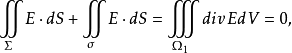因此从内部穿出曲面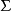的电通量

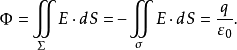
因此，电场强度穿出任一封闭曲面的电通量等于其内部的电荷量除以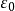，这正是电磁学中的Gauss定律。

此外，利用前面的讨论，电场强度的向量线(即电力线)应满足关系式

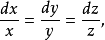由此解得电力线的方程为

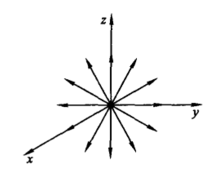
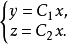这是一族从坐标原点出发的半射线(见图1)2。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学