预备知识数项级数的定义

给定一个数列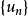 ，对它的各项依次用“+”号连接起来的表达式 “ 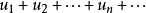” 称为数项级数，或称为无穷级数，也可以简称为级数，其中 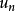称为数项级数的通项。

上述数项级数常写作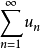： ，或者简单记作 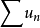。1

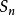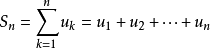数项级数的前n项和数项级数的前 n 项和记作 ，且有 。1

部分和数列称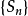数列 ，即数列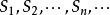 为数项级数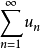 的部分和数列。1

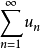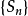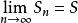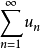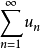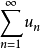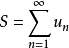定义若数项级数 的部分和数列 收敛于 （即 ），则称数项级数 收敛，即 为收敛级数，且称 为数项级数 的和，记作 。1

收敛级数分条件收敛级数和绝对收敛级数两大类，其性质与有限和（有限项相加）相比有本质的差别，例如交换律和结合律对它不一定成立，收敛级数概念是柯西于1821年引进的。

基本性质性质1设 k 为常数，如果级数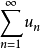 收敛于 ，则级数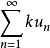 也收敛，且收敛于 。

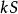证明：设级数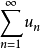 和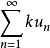 的部分和分别为 ，

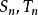则有 ，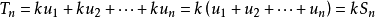

于是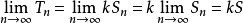 ，这就表明级数 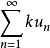也收敛，且收敛于 。

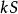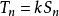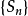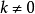注：由关系式 可知，如果数列 没有极限且 ，那么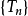 也没有极限。由此我们得到结论：级数的每一项同乘一个不为零的常数后，它的收敛性不变。2

性质2如果级数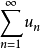 、 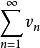分别收敛于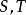 ，则级数 也收敛，且收敛到 。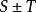

证明：设级数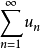 与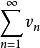 的部分和分别为 ，

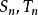则级数 的部分和为 ，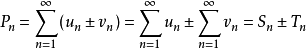

于是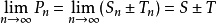 ，这就表明了级数 收敛，且收敛于 。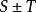

注意：性质2说明，两个收敛级数逐项相加或逐项相减之后仍为收敛级数。2

性质3在级数中去掉、加上或改变有限项，不会改变级数的收敛性。

证明：我们只需证明“在级数的前面部分去掉、加上有限项，不会改变级数的收敛性”，因为其他情形（即在级数中去掉、加上或改变有限项的情形）都可以看成在级数的前面部分先去掉有限项，然后再加上有限项的结果。

以去掉k项为例，设级数为 ，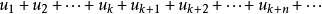

去掉前 k 项，得到新的级数 ，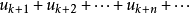

记原级数前 k+n 项的和为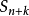 ，前 k 项和为 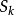，去掉前 k 项得到的新级数的前 n 项和为 ，

则有 。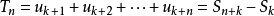

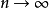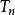易得当 时， 与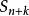 同时有极限，或者同时没有极限，

即级数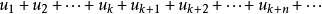 与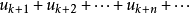 同时收敛或同时发散。

类似的，可以证明在级数前面加上有限项，不会改变级数的收敛性。2

性质4若级数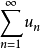 收敛，则对此级数的项任意加括号后所得的级数

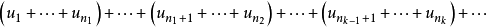
仍然收敛，且其和不变。

证明：设级数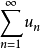 的前 n 项部分和 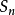，加括号后所成的级数的前 k 项的和为 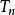，则有：

，

，

...

，

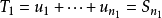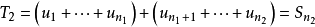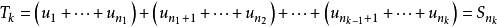可见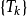，数列是数列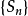的一个子数列。由数列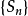的收敛性以及收敛子列与其子列的关系可知：数列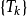必定收敛，且有。这说明了加括号后所成的级数收敛，且其和不变。

注意：如果加括号后所成的级数发散，则原级数也发散。2

性质5如果级数收敛，则必有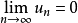。3

常用级数收敛性等比级数（几何级数）等比级数 ：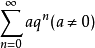

（1）当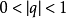 时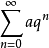，收敛，且收敛于；

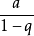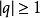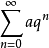（2）当时，发散。4

p级数p级数：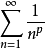

（1）当 p>1 时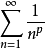，收敛；

（2）当 p ≤1时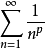，发散。4