研究历程
波兰数学家巴拿赫(S.Banach)和波兰数学家库拉托夫斯基(K.Kuratowski)于1920年证明了:若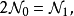 则在连续统上不存在(可数可加)测度,因而,可测基数的存在性不是简单的问题。研究可测基数,肇始于1930年的巴拿赫等人。两种可测基数之间有如下关系:首先,由定义可直接可得,二值可测基数必是实值可测基数。其次,美国数学家乌拉姆(S.M.Ulam)于1930年证明了,每个实值可测基数要么
则在连续统上不存在(可数可加)测度,因而,可测基数的存在性不是简单的问题。研究可测基数,肇始于1930年的巴拿赫等人。两种可测基数之间有如下关系:首先,由定义可直接可得,二值可测基数必是实值可测基数。其次,美国数学家乌拉姆(S.M.Ulam)于1930年证明了,每个实值可测基数要么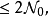 要么是二值可测基数。于是可推知,在广义连续统假设下,实值可测基数与二值可测基数相同。
要么是二值可测基数。于是可推知,在广义连续统假设下,实值可测基数与二值可测基数相同。
利用以色列学者索洛韦(R.M.Solovay)于1971年的结果可以证明,实值可测基数κ必是弱马赫罗基数,且小于κ的弱马赫罗基数组成κ的驻子集,乌拉姆早在1930年就证明了最小的可测基数≥最小的不可达基数。大约1960年,开斯勒(H.J.Keisler)和波兰学者塔尔斯基(A.Tarski)引入超积方法研究可测基数,证明了最小的可测基数比最小的不可达基数要大。另外,由于二值可测基数有树性质,于是得知,二值可测基数必是弱紧基数,若假设“存在二值可测基数”的大基数公理成立,则有如下这些关于可构造公理与广义连续统假设的结论:斯科特(D.S.Scott)于1961年用超幂方法证明了,若存在可测基数,则V≠L,即可构造公理不成立;罗伯托姆(F.Rowbottom)的下述结论更指出了大量的子集是不可构造的:若存在可测基数κ,则对每个满足ω≤λ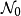 是κ-C(或κ-2)可测基数,则称κ是实值可测(或二值可测)基数,两者合称为可测基数。
是κ-C(或κ-2)可测基数,则称κ是实值可测(或二值可测)基数,两者合称为可测基数。
定义 设S是一无穷集,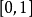 是单位闭区间,函数
是单位闭区间,函数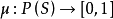 满足下列性质:
满足下列性质:
(i)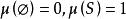 ;
;
(ii) 如果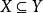 ,则有
,则有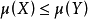 ;
;
(iii) 对所有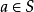 ,有
,有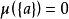 ;
;
(iv) 如果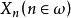 是两两不交的,则
是两两不交的,则
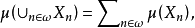 则称
则称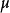 是S上的一个非平凡的、
是S上的一个非平凡的、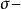 可加实值测度。其中(iii)表示其非平凡性,(iv)表示其
可加实值测度。其中(iii)表示其非平凡性,(iv)表示其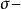 可加(即可数可加)性。若μ只取0,1二值,则称
可加(即可数可加)性。若μ只取0,1二值,则称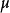 是S上的二值测度。
是S上的二值测度。
设μ是S上一二值测度,令
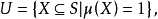 则U是S上的非主
则U是S上的非主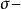 完全的超滤,反之,若U是S上
完全的超滤,反之,若U是S上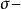 完全的超滤。函数
完全的超滤。函数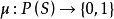 定义如下:
定义如下:
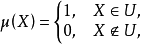 则μ又是S上的二值测度。
则μ又是S上的二值测度。
一般地,我们可以证明:如果μ是集S上的二值测度,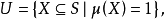 则μ是κ-可加的充要条件为U是κ-完全的。
则μ是κ-可加的充要条件为U是κ-完全的。
由于S上的κ-完全超滤和S上的κ-可加测度之间的这种内在联系,所以也把****超滤说成为测度。
研究实值可测基数,也是大基数研究中一个子课题,这里省略3。
相关性质定理引理S上的超滤U是κ-完全的充要条件为不存在S的r


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

