概念

位似形(homothetic figures)具有特殊位置的相似形。若两个图形F和F′的点之间可以建立一一对应关系，并且满足：1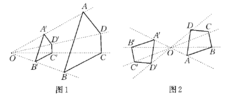

1.连结任一双对应点的直线都通过同一点O。

2.每双对应点均在点O的同侧(如图1)，或均在点O的异侧(如图2)。

3.对任一双对应点A和A′，有OA′/OA=k，

则称图形F和F′位似，或称图形F位似于图形F′，又称图形F和F′配景相似。图形F和F′称为位似图形或位似形，点O称为位似中心，对应点称为位似点，定比k称为“位似比”或位似系数，或位似率。当任一双对应点A，A′在点O的同侧，这时，图形F和F′称为顺位似图形，或称图形F和F′外位似，点O称为外位似中心，或外相似中心。这时规定位似比k>0。当任一双对应点A，A′在点O的两侧，这时图形F和F′称为逆位似，或称图形F和F′内位似，点O称为内位似中心，或内相似中心。这时规定位似比k0)。把这个映射叫做平面(空间)的相似变换。当k=1时，相似变换就是合同变换。相似变换保持两直线所成角的大小不变，并且不改变图形的形状而改变其大小，两个相似的平面图形，其面积之比等于它们的相似比的平方。位似变换是相似变换的特殊情形。对于平面到其自身的一个映射，如果存在定点S及常数K (K≠0)，使得对于任意点M及其象M’满足：①S，M，M’三点共线;②SM’=(K)SM，把这种映射称为以S为位似垂中心，K为位似比的位似变换。当 K>0时，对应的两点在位似中心的同侧，称为顺位似，S称为外位似中心;当K0时，点A和A′位于直线OA上点O的同侧，称这种位似变换为正向位似变换，或顺位似变换，O为外位似中心；当k1时，图形被放大，当|k|