概念

反同态(anti-homomorphism)是一类特殊映射。使运算反序的映射。设G与G′是两个群，f是G到G′的映射，若对任意的a，b∈G，f(b)f(a)=f(ab)，则称f是群G到群G′的一个反同态。若映射f还是一一映射，则称f为G到G′的反同构。特别地，当G′=G时，上述的反同态称为反自同态，反同构称为反自同构。

设E与F为两个群胚，f为从E到F中的映射。称f为从E到F中的反同态，如果f是从群胚E到F的反向群胚中的同态。这就等于说，对E的任一元素偶(x，y)，都有：2

f(x⊥y)=f(y)⊤f(x).

在幺半群，群或环的情况下有类似的定义。

映射映射亦称为函数。数学的基本概念之一。也是一种特殊的关系。设G是从X到Y的关系，G的定义域D(G)为X，且对任何x∈X都有惟一的y∈Y满足G(x，y)，则称G为从X到Y的映射。即关系G为映射时，应满足下列两个条件：

1.(x∈X)(y∈Y)(xGy).

2.(x∈X)(y∈Y)(z∈Y)((xGy∧xGz)→y=z)。这个被x∈X所惟一确定的y∈Y，通常表示为y=f(x)(x∈X)。f(x)满足：

1) f(x)∈Y.

2) G(x，f(x))成立(x∈X).

3)z∈Y，G(x，z)→z=f(x).

关系G常使用另一些记号：f：X→Y或XY。f与G的关系是y=f(x)(x∈X)，当且仅当G(x，y)成立。可取变域X中的不同元素为值的变元称为自变元或自变量。同样可取变域Y中的不同元素为值的变元称为因变元或因变量。始集X称为映射f的定义域。记为D(f)或dom(f)。终集Y称为映射的陪域，记为C(f)或codom(f)。Y中与X中的元素有关系G的元素的组合{y|x(x∈X∧y=f(x)∈Y)}称为映射的值域，记为R(f)或ran(f)。.当y=f(x)时，y称为x的象，而x称为y的原象。y的所有原象所成之集用f(y)表示。对于AX，所有A中元素的象的集合{y|x(x∈A∧y=f(x)∈Y)}或{f(x)|x∈A}称为A的象。记为f(A)。对于BY，所有B中元素的原象的集合{x|x∈X∧y(y∈B∧y=f(x))}称为B的原象。记为f(B)。显然：f(A)=f(x)，f(B)=f(y)。

群一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

同态设E与F为两个群胚，它们的合成法则分别记为⊥与⊤. 称从E到F中的映射f是群胚同态，如果对于E的任一元素偶(x，y)，有：

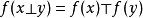
设E与F为两个幺半群(两个群)，称从E到F中的映射。f是幺半群(群)的同态，如果f是群胚的同态，且E的中性元素的象是F的中性元素。 (在群的情况下，后一个条件是自然满足的，但是从加法幺半群N到乘法幺半群N的映射x↦0是群胚的同态， 而并不因此就是幺半群的同态)。

设G为乘法群，而a为G的元素。由关系f(n)=an所定义的从加法群Z到G中的映射f是群的同态。

设A与B为两个环(两个体)，称从A到B中的映射f是环(体)的同态，如果f是加法群的同态，且为乘法么半群的同态. 这就是说，对A的任一元素偶(x，y)，有：

f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，

并且f将A的单位元变成B的单位元.

例如，设n为非零自然数；使任一有理整数对应其对模n的剩余类映射是从环Z到环Z/nZ上的同态。设E与F为两个A-代数(两个酉A-代数)。称从E到F中的映射f是A-代数(酉A-代数)的同态，如果它是线性映射，并且是乘法群胚(乘法幺半群)的同态。

例如，设E为交换体K上的非零有限n维向量空间，而B为E的基。则从E的全体自同态之酉代数ℒ(E)到K中元素构成的全体n阶方阵之酉代数Mn (K)中的映射，如果该映射使E的任一自同态对应它在基B中的矩阵，则这一映射是酉代数的同态。

同态的概念能用抽象的方式加以推广。

自同态指从群胚，幺半群，群，环到其自身中的同态，向量空间在自身中的线性映射，等等。

设G为关于加法的交换群。赋以加法及法则(f，g)↦g°f的G的全体自同态之集是一个环。

设E为交换体K上的向量空间。赋以法则(f， g)↦g°f， E的全体自同态之向量空间是酉代数，记为ℒ(E)，或End(E)。元素g°f仍记为gf。A-模的情形是类似的。

同构设E与F为两个群胚，两个幺半群，两个群，两个环，两个向量空间，两个代数或两个酉代数。称从E到F中的映射f是同构，如果f有逆映射，并且f与f是两个同态。 可以证明，任一双同态是同构。

设E与F为两个有序集。称从E到F中的映射f是同构，如果它存在逆映射，并且f与f-1都是递增的。即是说，对E的任一元素偶(x，y)，关系x≤y与f(x)≤f(y)等价。在E与F皆为全序集的情况下，可以证明任一双同态是同构。例如， 指数函数x↦ex是从实数加法群R到严格正实数乘法群R*+上的同构。逆同构是对数函数x↦lnx。 二者都是递增的，这两个双射也是有序集的同构。3

自同构设E为群胚，幺半群，群，环，向量空间，代数或酉代数。从E到其自身上的同构称为E的自同构。

赋以合成法则(f，g)↦g°f后，E的自同构集是一个群，自然地称为E的自同构群，记为Aut(E).例如，设E为交换体K上的向量空间. E的同位相似是自同构，当且仅当它的比不为零。 ——现假定E为有限维的。为使E的自同态是自同构，必须且只须它是单射，或是双射。