概念

算子同态(operator homomorphism)是指一般群的同态，是同构在算子群上的推广。设G1，G2为两个算子群，Ωi分别为Gi的算子集 (i=1，2)。若G1与G2同态，Ω1与Ω2之间存在一一映射α1α2(αi∈Ωi，i=1，2)，使得在G1与G2的同态下，即当gi∈Gi(i=1，2)，g1→g2时恒有g1→g2，则称G1与G2关于Ω1，Ω2是算子同态的。当上述G1与G2间的同态为同构映射时，称G1与G2为算子同构，记为：1

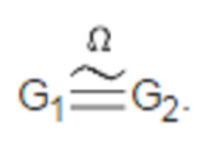
算子同态(同构)又称为Ω同态(同构)，或容许同态(同构)。

群群是一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

算子群算子群亦称带算群或称Ω群。比群更广且有重要运用价值的群类。群G到G的一个映射α：gg称为G的一个算子，若对于任意的x，y∈G，均有(xy)=xy。G的一个算子就是G的一个自同态。G的某些算子做成的集合，称为G的一个算子集.算子集常用Ω记。带有算子集的群称为带算群，或算子群，或Ω群。设H是群G的子群，Ω是G的一个算子集，若对任意的α∈Ω，h∈H，均有h∈H，则称H是G的Ω容许子群(Ω不变子群)。当Ω是G的全体内自同构所成之集时，G的Ω容许子群就是G的正规子群；当Ω是G的全体自同构所成之集时，G的Ω容许子群就是G的特征子群。算子群的理论与一般群的理论是平行的，群的一般理论都可以推广到算子群上去，且取定适当的算子集，有时还可以提高对群本身的研究效果。而一般的群可以看成算子集为空集的群。

同态设E与F为两个群胚，它们的合成法则分别记为⊥与⊤。称从E到F中的映射f是群胚同态，如果对于E的任一元素偶(x，y)，有：2

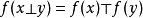
设E与F为两个幺半群(两个群)，称从E到F中的映射。f是幺半群(群)的同态，如果f是群胚的同态，且E的中性元素的象是F的中性元素。(在群的情况下，后一个条件是自然满足的，但是从加法幺半群N到乘法幺半群N的映射x↦0是群胚的同态， 而并不因此就是幺半群的同态)。

设G为乘法群，而a为G的元素。由关系f(n)=an所定义的从加法群Z到G中的映射f是群的同态。

设A与B为两个环(两个体)，称从A到B中的映射f是环(体)的同态，如果f是加法群的同态，且为乘法么半群的同态。这就是说，对A的任一元素偶(x，y)，有：

f(x+y)=f(x)+f(y)f(xy)=f(x)f(y)，

并且f将A的单位元变成B的单位元。

例如，设n为非零自然数；使任一有理整数对应其对模n的剩余类映射是从环Z到环Z/nZ上的同态。设E与F为两个A-代数(两个酉A-代数)。称从E到F中的映射f是A-代数(酉A-代数)的同态，如果它是线性映射，并且是乘法群胚(乘法幺半群)的同态。

例如，设E为交换体K上的非零有限n维向量空间，而B为E的基。 则从E的全体自同态之酉代数ℒ(E)到K中元素构成的全体n阶方阵之酉代数Mn (K)中的映射，如果该映射使E的任一自同态对应它在基B中的矩阵，则这一映射是酉代数的同态。

同态的概念能用抽象的方式加以推广。

群的同态一类重要的映射。群之间的保持运算的一类映射。设f是群G到群G′(不必异于G)的映射，若f保持运算，即对所有的x，y∈G，总有f(xy)=f(x)f(y)(或(xy)=x·y)，则称f是群G到群G′的同态映射，简称同态。若同态映射f还是一个双射，则称f为G到G′的同构映射，记为GG′.这时称群G和G′同构，记为GG′。特别地，若G=G′时，则分别称f为群G的自同态和自同构。

同构两个数学系统(例如两个代数系统)，当它们的元素及各自所定义的运算一一对应，并且运算结果也保持一一对应，则称这两个系统同构，记为≌。它们对于所定义的运算，具有相同的结构。例如，十进制数与二进制数是同构的。

建立同构关系的映射，称为同构映射。例如，当映射为一一映射，并且对应元素关于运算保持对应时，就是同构映射。

同构是数学中最重要的概念之一。在很多情况，一个难题往往可以化成另一个同构的、似乎与它不相关的、已经解决的问题，从而使原问题方便地得到解决。虽然数学发展得越来越复杂，但利用同构概念，不仅使数学得到简化，而且使数学变得越来越统一。表面上似乎不同，但本质上等价的结果，可以用统一的形式表达出来。例如，如果四色定理得到了证明，其他数学分支中与它同构的几十个假设，也同时得到了证明。3