一个有限射影几何包含着由点P、q、…组成的有限集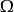 以及由
以及由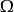 的子集L、M、……组成的子集簇,这些子集称为线,并且这些子集满足公理(i)一(iv)(若
的子集L、M、……组成的子集簇,这些子集称为线,并且这些子集满足公理(i)一(iv)(若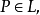 ,我们称P在L上或L通过P)。1
,我们称P在L上或L通过P)。1
(i) 通过任意两不同的点P和q存在唯一的一条线(用(Pq)表示)。
(ii) 每条线至少包含3点。
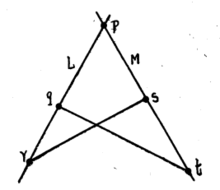
(iii) 若不同的线L,M有公共点P,且若q,r为L上不等于P的点,及s,t为M上不等于P的点,则线(qt)和(rs)也有一公共点(看图1)。
(iv) 对任意点P至少存在两条不含P的线,而对任意线L至少存在两个不在L上的点。
射影几何的子空间必是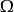 的子集S且S满足:
的子集S且S满足:
(v) 若P,q是S的不同的点则S包含线(Pq)上所有的点。
子空间的实例就是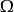 内的点和线以及
内的点和线以及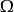 自身。超平面H是最大的正规子空间,所以
自身。超平面H是最大的正规子空间,所以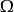 是唯一的完全包含H的子空间。
是唯一的完全包含H的子空间。
定义 从一射影几何的子空间中去掉一固定的超平面H(叫做在无穷远处的超平面)的点就得到一仿射或欧几里德几何。所形成的那些集都叫做仿射几何的子空间。
在一射影几何或仿射几何中的一点集t,若对一切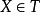 ,则X不属于包含T-{X}的最小子空间,T叫做独立的。例如,任何不在一线上的三点啤做独立的。如果 r 是在子空间S中独立点的最大集的尺度,S的维数是r-1。特别地,若S=
,则X不属于包含T-{X}的最小子空间,T叫做独立的。例如,任何不在一线上的三点啤做独立的。如果 r 是在子空间S中独立点的最大集的尺度,S的维数是r-1。特别地,若S=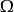 这就定义了射影几何的维数。
这就定义了射影几何的维数。
射影几何PG(m,q) 射影几何和仿射几何中最重要的是从有限域得到的那些情况。
设GF(q)为一有限域且假定m≥2.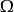 的点以非0的(m+1)重
的点以非0的(m+1)重
 表示,并且规定
表示,并且规定
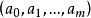 和
和
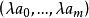 代表相同的点,这里
代表相同的点,这里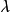 为GF(q)的任意非0元。这些叫做点的齐次坐标。存在
为GF(q)的任意非0元。这些叫做点的齐次坐标。存在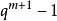 个非0的(m+1)重而每点出现q-1次,所以在
个非0的(m+1)重而每点出现q-1次,所以在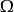 中点的数目为(
中点的数目为(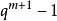 )/(q一1)。
)/(q一1)。
通过两不同点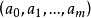 和
和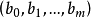 的线由点
的线由点
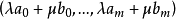 构成,这里
构成,这里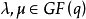 均不为0。因为对于
均不为0。因为对于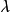 ,
,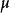 存在q2—1种选择而每点在上式中出现q-1次,一线包含q十1点。
存在q2—1种选择而每点在上式中出现q-1次,一线包含q十1点。
明显地满足公理(i),(ii)。1
仿射平面上的直线作为有限域的一个应用,下面介绍有限几何的概念。
定义1 设F是有限域,仿射平面AP(F)由下列两个集合组成:
① 点集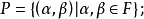 ,
,
② 直线集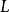 ={
={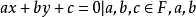 不全为0}。
不全为0}。
不难证明仿射平面AP(F)具有普通欧几里得平面的性质:
① 过两个不同的点只能作一条直线;
② 过一直线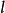 外的点P只能作一条直线
外的点P只能作一条直线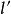 与
与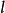 不相交。
不相交。
由于AP(F)是定义在有限域上,因而P与L都是有限集合,且有以下计数定理。
定理1 设F是有限域且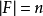 ,AP(F)是F上的仿射平面,则有
,AP(F)是F上的仿射平面,则有
①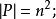
②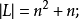
③ 每条直线恰通过n个点;
④ 每个点恰在n+1条直线上。
有限域理论在组合设计中有很好的应用。
离散椭圆曲线有一种密码系统是利用离散椭圆曲线进行编码的,那么什么是椭圆曲线呢?我们先从实平面上的椭圆曲线说起,设a,b为实数,实平面上的曲线方程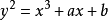 的图形是以x轴为对称轴的曲线,称为椭圆曲线(elliptic curve).根据判别式
的图形是以x轴为对称轴的曲线,称为椭圆曲线(elliptic curve).根据判别式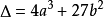 的三种情况
的三种情况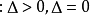 和
和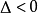 ,椭圆曲线有三种类型。例如,方程
,椭圆曲线有三种类型。例如,方程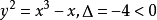 ,曲线由两部分组成,在左半平面是一个类似于椭圆的一条封闭曲线,而右半平面是一条不封闭的趋向无穷的曲线。
,曲线由两部分组成,在左半平面是一个类似于椭圆的一条封闭曲线,而右半平面是一条不封闭的趋向无穷的曲线。
类似,我们可以在有限几何中研究椭圆曲线,它的定义如下。
定义2 设p>3为素数,有限域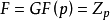 ,
,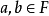 且
且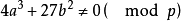 ,则满足同余式
,则满足同余式
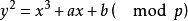 的点
的点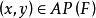 的集合E称为F上的离散椭圆曲线(discrete elliptic curve).并假定E中有一个特殊点O。在E中定义加法
的集合E称为F上的离散椭圆曲线(discrete elliptic curve).并假定E中有一个特殊点O。在E中定义加法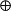 如下:设
如下:设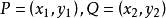 ,则
,则
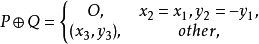 其中
其中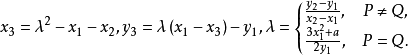
定义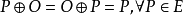 。
。
上面式子中的运算均为mod p的运算。
可以证明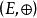 是可换群.元素
是可换群.元素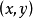 的逆元为
的逆元为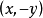 。
。
各种形式的同余方程在密码学中有很多应用,对于指数是未知数的同余方程,就是所谓离散对数(discrete logarithm)问题:
定义3 设p>3为素数,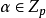 是一个本原元,
是一个本原元,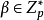 ,求整数
,求整数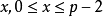 满足
满足
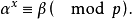 x存在且惟一的,称x为
x存在且惟一的,称x为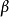 的以
的以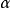 为底的离散对数,并记作
为底的离散对数,并记作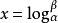 。
。
首先我们看一下离散对数的存在惟一性.这是因为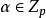 是一个本原元,它是
是一个本原元,它是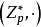 的生成元,所以
的生成元,所以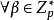 均有
均有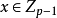 使
使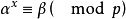 .若有J
.若有J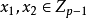 ,则由
,则由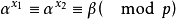 得
得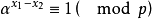 ,因而
,因而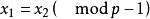 ,在[0,p-2]范围内是惟一确定的。
,在[0,p-2]范围内是惟一确定的。
我们更关心的是如何计算离散对数.由于是在有限域上计算离散对数,自然会想到把所有的幂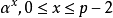 都计算出来,从而找出
都计算出来,从而找出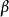 所对应的x。2
所对应的x。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

