分次模(graded module)是具有分次结构的分次环上的模,是同调代数的基本概念之一,指由一些A模所组成的序列。类似于分次环,在分次模中可定义g分支、g次齐次元和g次齐次分量。分次模M的支集规定为{Mg≠0|g∈G},并记为SuppG(M)。M的G分次子模N,是指N为M的R子模且N=⊕g∈G(N∩Mg),这等价于若x∈N,则x的齐次分量也在N中,特别地,RR的分次子模称为R的分次左理想,类似地,可定义R的分次右理想和分次理想1。
基本介绍分次模(graded module (in homological algebra) )是同调代数的基本概念之一,指由一些A模所组成的序列。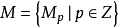 称为一个(单)分次模,其中
称为一个(单)分次模,其中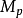 均为A模,环A上的一个复形
均为A模,环A上的一个复形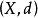
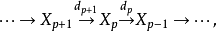 若不考虑边缘同态d,则决定一个分次模
若不考虑边缘同态d,则决定一个分次模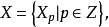 若
若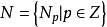 也是一个分次模,n是一个固定的整数,则模同态
也是一个分次模,n是一个固定的整数,则模同态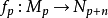 的集合
的集合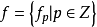 称为由M到N的n次的分次模映射,这个映射常表成
称为由M到N的n次的分次模映射,这个映射常表成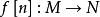 。若分次模
。若分次模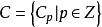 中,对每个
中,对每个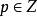 都有
都有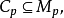 称
称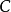 为
为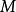 的分次子模,而分次模
的分次子模,而分次模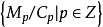 称之为它们的分次商模。模范畴
称之为它们的分次商模。模范畴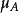 中所有的分次模连同分次模映射构成一个阿贝尔范畴1。
中所有的分次模连同分次模映射构成一个阿贝尔范畴1。
①A是Noether 环,M是有限生成的A-模,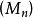 是M的一个
是M的一个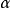 -滤链,则下述论断等价:
-滤链,则下述论断等价:
i)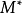 是有限生成
是有限生成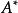 -模;
-模;
ii) 滤链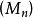 是稳定的。
是稳定的。
②(Artin-Rees引理)设A是Noether环,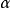 是A的一个理想,M是一个有限生成的A-模,
是A的一个理想,M是一个有限生成的A-模,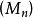 是M的一个稳定
是M的一个稳定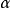 -滤链,设
-滤链,设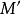 是
是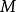 的一个子模,则
的一个子模,则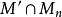 是
是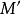 的一个稳定
的一个稳定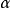 -滤链。
-滤链。
③存在整数k,使得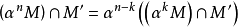 ,对一切
,对一切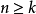 。
。
④设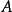 是Noether环,
是Noether环,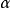 是一个理想,
是一个理想,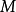 是一个有限生成A-模,
是一个有限生成A-模,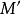 是
是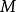 的一个子模,则滤链
的一个子模,则滤链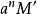 和
和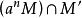 具有有界差。特别,
具有有界差。特别,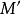 的
的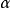 -拓扑与由
-拓扑与由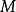 的
的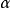 -拓扑所诱导出的拓扑相同。
-拓扑所诱导出的拓扑相同。
⑤设
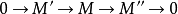 是Noether 环A上有限生成的正合序列是,
是Noether 环A上有限生成的正合序列是,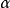 是A的理想,则
是A的理想,则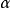 -adic完备化序列
-adic完备化序列
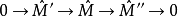 是正合的。
是正合的。
⑥设A是Noether环,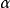 是一个理想M是有限生成A-模,
是一个理想M是有限生成A-模,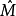 是M的
是M的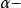 完备化,则
完备化,则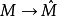 的核
的核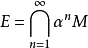 由M中被
由M中被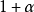 中某元素所零化的那些元素x组成。
中某元素所零化的那些元素x组成。
⑦A是Noether环,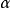 是A的一个包含在大根中的理想。M是有限生成A-模,则M的
是A的一个包含在大根中的理想。M是有限生成A-模,则M的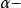 拓扑是Hausdorff 拓扑,即
拓扑是Hausdorff 拓扑,即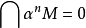 。
。
⑧设A是Noether局部环,m是它的极大理想,M是有限生成A-模,则M的m-拓扑是Hausdorff 拓扑,特别A 的m-拓扑是Hausdorff 拓扑2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

