概念

有向群(directed group)是一类特殊的偏序群。设G是偏序群，若G具有性质：对任意a，b∈G，存在c∈G，使得：

a≤c， b≤c，

则称G为有向群。偏序群是有向群，当且仅当它作为偏序集是有向集。任意格群都是有向群。2

群一种只有一个运算的、比较简单的代数结构；是可用来建立许多其他代数系统的一种基本结构。

设G为一个非空集合，a、b、c为它的任意元素。如果对G所定义的一种代数运算“·”(称为“乘法”，运算结果称为“乘积”)满足：

(1)封闭性，a·b∈G;

(2)结合律，即(a·b)c = a·(b·c);

(3)对G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，则称G对于所定义的运算“·”构成一个群。例如，所有不等于零的实数，关于通常的乘法构成一个群;时针转动(关于模12加法)，构成一个群。

满足交换律的群，称为交换群。

群是数学最重要的概念之一，已渗透到现代数学的所有分支及其他学科中。凡是涉及对称，就存在群。例如，可以用研究图形在变换群下保持不变的性质，来定义各种几何学，即利用变换群对几何学进行分类。可以说，不了解群，就不可能理解现代数学。

1770年，拉格朗日在讨论代数方程根之间的置换时，首先引入群的概念，而它的名称，是伽罗华在1830年首先提出的。

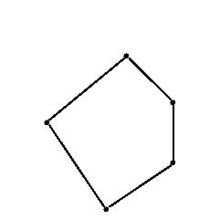
偏序集偏序集是特定的集。它是一类主要的序关系集。具体地说，集合E连同其上的偏序R构成的关系集(E，R)，一般记为P=(E，≤)。所谓偏序(或序关系)是一类具有自反性、反对称性和传递性的二元关系。例如，数之间的不大于关系，自然数之间的整除关系，集合之间的包容关系等。把集合E的基数称为偏序集P的阶。阶为有限值的偏序集称为有限偏序集。而在P上，对于任意元素x，y，区间[x，y]均为有限偏序集时，称P为局部有限偏序集.这两类偏序集是组合理论中的主要研究对象.偏序集上所有链的长度的最小上界，或上确界，称为偏序集的长度，记为l(P)。偏序集中最大反链包含的元素数目，称为偏序集的宽度，记w(p)。对于以右图为哈塞图的偏序集P，有l(P)=3，w(P)=2.偏序集的子关系集仍为偏序集，而且必有全序集作为其子关系集。3

设A是一个集合，若在A内存在一个关系“≤”，它满足：

①反身性 对于任何a∈A，有a≤a；

②反对称性 对于a，b∈A，若a≤b，且b≤a，则a=b；

③传递性 对于a，b，c∈A，若a≤b，b≤c，则a≤c。

则称“≤”是集合A的一个偏序关系，也称作半有序关系。

如果a≤b，就叫做a不在b的后面，或b不在a的前面。

在一个集合A内，如果建立了一个偏序关系≤，就称集合A对于关系≤成为一个偏序集，也称作半有序集.记作(A，≤)。

由上述定义可知，偏序集就是一个集合A加上一个偏序关系≤。

例如，实数集R对于关系“≤”构成偏序集(R，≤)。

再如，设I是一个全集，幂集P(I)对于关系“⊂”是一个偏序关系，(P(I)，⊂)是一个偏序集。值得注意的是，当A，B⊂P(I)，且A∩B=Φ时，A⊂B和B⊂A都不成立，但这不要紧，因为定义中不要求对于A中的任意两个元素a和b，a≤b或b≤a必有一个成立，这就是说，它只要求这种顺序关系≤在部分元素中成立。4

偏序群偏序群亦称半序群。一种具有序结构的群。自从第二次世界大战以后，随着伯克霍夫(Birkhoff，G.D.)、罗伦岑(Lorenzen，P.)等人的基础文章的发表，格序群成为一门学科。康莱德(Conrad，P.)于1960年发表的文章中提供了利用凸子群来研究格序群类结构的工具。这个方法特别成功的例子是他的学生哈韦(Harvey，J.)、赫兰(Holland，W.C.)将哈恩(Hahn，H.)关于可换格序群的嵌入定理推广到一般的格序群。设(G，+，0)是群，若G又是偏序集，且偏序≤对加法是相容的，即对任意x，y，a，b∈G，由x≤y得a+x+b≤a+y+b，则称G为偏序群。偏序群的任意子群关于此偏序群的偏序是一个偏序群。例如，若X是拓扑空间，C(X)为X上所有实值连续函数加群，对任意f，g∈C(X)，定义f≤g当且仅当对任意x∈X，f(x)≤g(x)，则C(X)是一个偏序群。

格序群

亦称格群或l群。一种具有格序关系的群。若偏序群G作为偏序集是格，则称G为格序群。格群是分配格。设G既是群又是格，则G是格序群当且仅当对任意a，b，x，y∈G，满足：

a+(x∨y)+b=(a+x+b)∨(a+y+b)，

a+(x∧y)+b=(a+x+b)∧(a+y+b).

除去平凡的格群外 ，没有有限格群。5