伽罗瓦预解式1(Galois resolvent)，是决定方程的伽罗瓦群的一个函数式。

伽罗瓦2(Galois，Evariste)，法国数学家。法国数学家。他发现每个代数方程必有反映其特性的置换群存在。从而解决了用根式解代数方程的可能性问题，创立了“伽罗华理论”，并为群论的建立、发展和应用奠定了基础。

定义伽罗瓦预解式1(Galois resolvent)是决定方程的伽罗瓦群的一个函数式。设域F上的n次多项式f(x)没有重根，且x1，x2，…，xn为其根。可选择m1，m2，…，mn使得函数

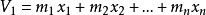
在x1，x2，…，xn的n!个置换作用于V1能够得到n!个不同的函数V1，V2，…，Vn!。再构造一个函数。

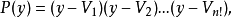
它作为y的多项式，其系数为V1，V2，…，Vn!的初级对称多项式，当然也为根x1，x2，…，xn的对称函数，若P(y)在F上不可约，则取G(y)=P(y)；若P(y)在F上可约，规定G(y)是P(y)的以V1为根的不可约因式。这个不可约多项式G(y)就称为f(x)=0的伽罗瓦预解式。由于G(y)的根是V1，V2，…，Vn!的一部分，所以，若V1，V2，…，Vs为s次多项式G(y)的根，则由V1变为V1，V2，…，Vs所对应的s个置换σ1，σ2，…，σs构成n次对称群Sn的一个子群，这个子群同构于f(x)=0的伽罗瓦群。

起源与发展背景19 世纪初3，在解出三、四次方程后的整整两个半世纪内，很少有人去怀疑五次以及五次以上的代数方程的根式求解的可能性。拉格朗日(J．L．Lagrange，1736—1813)的目标是完成一般方程的根式解问题，而高斯(Carl FriedrichGauss，1777—1855)的工作只给出了一类特殊方程的根式解。历史上第一个明确提出“不可能用根式解四次以上方程”的数学家是拉格朗日。1770 年，在《关于代数方程解的思考》一文中，讨论了在他之前人们所熟知的解二、三、四次方程的一切解法，并且指出这些成功解法所根据的情况对于五次以及更高次方程是不可能发生的。

受拉格朗日的影响，鲁菲尼(Ruffini，1765—1822)在其著作《方程的一般理论》中，证明了不存在一个预解函数能满足一个次数低于五次的方程。后来，他大胆地着手证明，五次及五次以上的代数方程是没有根式解的。但是，鲁菲尼的证明晦涩难懂，故当他的成果发表之后，得到了许多负面评论，甚至不断有人否认他的工作。

1824年，阿贝尔作出了一个新的证明，这个证明于1826年发表在克雷尔(L． Crelle，1780—1855)杂志上，题为“论五次代数方程”。尽管这个证明同样包含了一些小错误，但却本质上解决了一般五次及五次以上方程不存在根式解。

创建在鲁菲尼和阿贝尔之后，关于代数方程的根式解工作被分成了有着完全不同结果的两类：一类是任意次分圆方程的可根式求解；另一类是五次及五次以上一般方程的不可根式解。因此，数学家面临的问题产生了：哪一类特殊方程是可以根式求解的？

这个问题被年轻的数学家伽罗瓦所解决。伽罗瓦的论文曾遭到法国科学院的冷遇，直到他去世以后，在1846年才由刘维尔(J．Liouville，1809—1882)整理发表出来。

思想方法为了掌握伽罗瓦的思想，在此考虑方程：

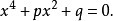
其中系数p，q是独立的，令F是由p，q的有理表达式所形成的域，这些表达式的系数在有理域中，一个典型的表达式是

这个方程的4个根是：

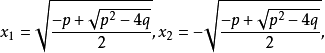
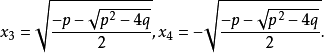
容易看出这些根的系数在F中的两个关系x1+x2=0，x3+x4=0对这些根都成立。因为是四次方程，因而有根的总共24个可能置换。下面8个置换：

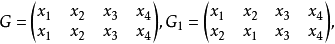
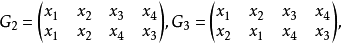
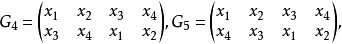
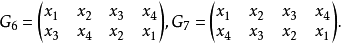
都能使上述两个关系在F中保持成立，并且这8个置换是24个置换中使根之间在域F中的全部代数关系都保持不变的仅有的变换。这8个置换就是方程在域F中的群，即伽罗瓦群。这是历史上最早的“群”的定义。不过这不是抽象群的一般定义，它只是针对一个具体的群（置换群）所作的定义。但是，伽罗瓦正是利用这个“群”的定义解决了方程根式可解性问题。

接着伽罗瓦证明了当一个方程关于给定域的群恰是G时，方程的各个根都属于这个域。因此，若根在域 F'''中，因F'''是通过将已知域F用逐次添加已知量得到的，所以可知根所在的这个域F，另外，还可用F'''中有理运算来直接找方程的根。

伽罗瓦给出了一个方法来找给定方程的群、逐次的预解式以及方程关于逐次扩大了的系数域的群，即原来群的逐次子群，而扩大的系数域是由添加这些逐次的预解式的根到原来的系数域而得到的。

通过这个方法，我们能从最初的域通过逐次添加根式过渡到根所在的最后的域。反之，如果一个方程能用根式求解，则预解式方程组必定存在，而且必定是二项方程。

影响在伽罗瓦3的思想方法中，他引进了许多具有决定意义的概念，在此论述最为重要的一些内容。

一、“伽罗瓦群”概念的提出。假设由方程的系数生成的域记为F，E是方程的根域，它是将方程的根添加到F上所生成的扩域，称之为伽罗瓦扩张。伽罗瓦注意到，每个方程的伽罗瓦扩张都可以与某一个置换群联系起来，这个置换群中的每个元素都是将伽罗瓦扩张中的元素置换到伽罗瓦扩张中的元素，并且保持 F 中的元素不变。我们将这些置换构成的群称为伽罗瓦群。可以看出，对于任一个关于根的有理多项式函数，伽罗瓦群中的每个置换都使这个值不变；反之，若伽罗瓦群中的每个置换都使一个根的多项式函数的值不变，那么这个多项式函数是有理的。因此，一个方程的伽罗瓦群完全体现了它的根的整体对称性。当时伽罗瓦正是发现并证明了这个充要条件，进而提出了现代课本中的“伽罗瓦群”这一重要概念的。

二、是“正规子群”和“可解群”的概念。当时伽罗瓦称之为“真分解”，即群G的子群H叫作G的正规子群，是指对于每个g∈G，g-1Hg=H，记为H◁G。正是因为伽罗瓦弄清楚了正规子群的结构和性质，才使他建立代数方程根式可解性理论成为可能。

三、伽罗瓦注意到，每个方程是否可用根式解的关键，是这个方程系数所在的域F能否通过有限次添加根式而扩张成为根域E。在发现了这种域和群之间的对应关系以后，他便提出并且证明了方程存在根式解的著名判断准则：域F上的一元n次方程有根式解的充要条件是方程的伽罗瓦群是可解群。这一准则称为伽罗瓦判别定理，它所描述的域和群之间的对应在现代课本中称为“伽罗瓦对应”。伽罗瓦正是发现了这种一一对应关系，并且利用这种对应关系才最终解决了代数方程根式可解性理论这一历史难题。

名人介绍伽罗瓦2(Galois，Evariste)，法国数学家。生于巴黎郊区布拉伦(Bourg-la-Reine)，卒于巴黎。幼时受到良好的家庭教育。12岁入中学，在数学教师理查德(Richard 1795—1849)指导下研究代数方程可解条件问题，17岁（1828年）高中未毕业便写出了关于循环连分数及五次方程代数解法的论文。18岁（1829年）中学毕业，同年进入师范学校。他是法国资产阶级革命的积极参加者，曾因此被开除学籍并两次入狱。恢复自由后不久，因政治和爱情的纠葛，在一次决斗中不幸身亡，年仅21岁。

伽罗瓦短暂的一生，为数学增添了全新的思想，如群、域概念发展成为了许多新的数学分支。特别是还发现了每个代数方程必有反映其特性的置换群存在，从而解决了多年不能解决的用根式解代数方程的可能性的判断问题，创立了“伽罗瓦理论”，并为群论的建立、发展和应用奠定了基础。也使他成为了19世纪伟大的数学家之一。

1830年与1831年，伽罗瓦写出了两篇关于方程论的重要论文，提交给了法国科学院，但因受权威压制，未能发表。直到他死后14年，即1846年，法国数学家刘维尔(Liouville，J.)才发现他的遗作的巨大意义，将他的遗稿汇集出版。1870年，法国数学家若尔当(Jordan，M.E.C.)还根据伽罗瓦的思想写出了《置换与代数方程》一书。

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学