定义
与单点空间同伦等价的拓扑空间称为可缩空间(contractible space),这是伦型最简单的一类空间。可缩空间是道路连通的(因为它与道路连通的单点空间同伦等价),并且具有平凡的基本群,因而是单连通的。2
相关性质下面的定理是可缩性的等价刻画。
定理1 空间X是可缩的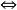 X到自身的恒同映射是零伦的.即
X到自身的恒同映射是零伦的.即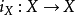 与常值映射
与常值映射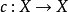 同伦(
同伦(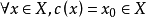 )。 -
)。 -
证明: (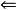 ) 设
) 设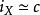 ,记
,记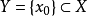 ,令
,令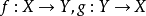 使得
使得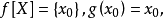 则
则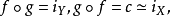 故X与
故X与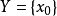 同伦等价,即X是可缩的。
同伦等价,即X是可缩的。
(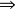 ) 设X是可缩的,则有
) 设X是可缩的,则有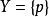 及同伦等价映射
及同伦等价映射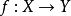 及
及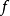 的同伦逆
的同伦逆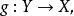 记
记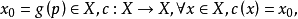 ,则
,则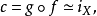 故X到自身的恒同映射是零伦的。3
故X到自身的恒同映射是零伦的。3
命题 如果X是可缩空间,则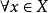 都是X的形变收缩核。
都是X的形变收缩核。
证明 记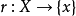 .由于X是可缩空间,因而r是同伦等价,又由于X是道路连通的,故从{x}到X的映射类只有一个,由此可见,每一个映射
.由于X是可缩空间,因而r是同伦等价,又由于X是道路连通的,故从{x}到X的映射类只有一个,由此可见,每一个映射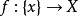 都是r 的同伦逆.特别地,含入映射
都是r 的同伦逆.特别地,含入映射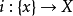 也是r的同伦逆,即有
也是r的同伦逆,即有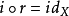 ,因此{x}是X的形变收缩核。2
,因此{x}是X的形变收缩核。2
例题解析例1 (1)显然,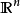 及
及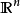 中的凸集都是可缩空间;
中的凸集都是可缩空间;
(2) 对于任何拓扑空间X,由于锥顶是拓扑锥CX的强形变收缩核,因此拓扑锥CX都是可缩空间。
例2 现在我们来描述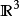 的一个2-维子空间X(称为有两个房间的屋子),它是可缩的,但不是以一种很明显的方式。
的一个2-维子空间X(称为有两个房间的屋子),它是可缩的,但不是以一种很明显的方式。
为了构造这个空间,从一个被一个水平长方形分成两个小室的盒子开始,这里所谓“长方形”不只指它的四条边,还包括其内部,借由两个垂直通道,可以从盒子外面进入两室,上部的通道是通过在盒子的顶部打开一个正方形口子,在其正下方的水平长方形上打开另一个正方形口子,然后插入四个铅直的长方形作为通道壁,这个通道可以从盒子外部进入下室,下部的通道用类似的方法做成,为进入上室提供了一个入口,最后插入两个铅直的长方形形成两个通道的“支撑墙”,因此所得的空间X由三个同胚于圆环的水平片加上构成两室的墙壁的所有铅直长方形构成(如图1(a),(b)所示)。
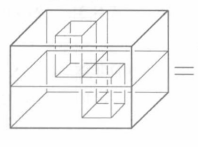
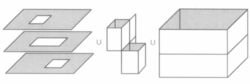
为了看出X是可缩的,考虑X的 一个闭的ε-邻域N(X),如果ε足够小,这显然可以形变收缩到X上,事实上,N(X)是从N(X)的边界曲面到X上的 一个映射的映射柱,为了看出这一点,想象从一个黏土球制作N(X):将一个手指伸人球内做出上通道,然后慢慢地挖空下室;接着类似地伸入一个手指做出下通道,并挖空上室,从数学上来讲,这个过程给出了一族嵌人映射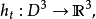 以通常的含入
以通常的含入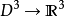 开始,以到N(X)上的 一个同胚结束,可见X是可缩的。
开始,以到N(X)上的 一个同胚结束,可见X是可缩的。
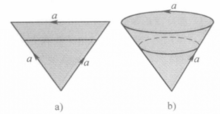
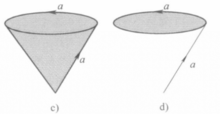
例3 三角开的三条边按如图2(a)所示的那样进行粘接,得到所谓的“蜷帽”,记做Q,则Q也是可缩的.Q可以看成一个圆锥体的侧面粘合底边与一条母线而得的商空间(如图2(b)).现在作圆锥体的商空间S,它是把圆锥体的底边与一条母线粘合而得的商空间(如图2(c)),由于圆锥体的侧面是圆锥体的强形变收缩核,因而Q 是S 的强形变收缩核,由于S可强形变收缩为图2(d) 中的图形,而后者实际上是一个圆盘,显然是可缩的。因此S 是可缩的,从而Q 也是可缩的。2


 科普中国公众号
科普中国公众号
 科普中国微博
科普中国微博

 帮助
帮助

